Cómo montar el sextante, de Tycho Brahe (1598).
Tycho Brahe muestra cómo montar el sextante para medir la elevación de los objetos celeste; (de Astronomiæ instauratæ mecanica, Wandsbek 1598). AMJ
Curiosidades IX-(Ene-2018-->)
¡¡El premio "Gordo" de la Lotería de Navidad tenía que ser primo...!!
Aunque algunos hemos hecho el "primo", este número se ha comportado "primorosamente". AMJ
Decía Paul Klee: "Una línea es un punto que fue a caminar".
"Klee estaba obsesionado con el orden y los números" dicen de él. Su obra lo corrobora.(Ya tenemos una entrada en este blog: Paul Klee y la Geometría. )AMJ
¡Geometría por los suelos!
 |
|
¡La geometría ayuda en el supermercado!
Estos envases para huevos, diseñados con ayuda geométrica, permiten su trato y protección individuales, además de utilizar el mínimo espacio. (Visto en taringa.net). AMJ
Decorando con círculos.
Preciosa vasija de cerámica adornada con círculos. AMJ
¿Qué hace falta para ser un buen profesor?
Extraordinario. AMJ
Para desayunar... matemáticas.
 |
|
(de @ydanard) AMJ
π en el triángulo de Pascal, de Daniel Hardisky.
EL triángulo de Pascal encierra multitud de series que nos acercan a resultados increíbles. Con una variación sobre la serie de Nilakantha Somayaji, matemático hindú(1444,1544), Hardisky encontró esta maravilla. AMJ
The Rolling Bridge, el puente que se convierte en un octógono.
Al oeste de Londres, en Paddington Basin, tenemos este puente, The Rolling Bridge, que su peculiaridad consiste en enrollarse formando un octógono. La construcción se basa en 8 porciones triangulares de acero y madera y se cierra y abre por medio de bombas hidráulicas. El tiempo total para la apertura o cierre es de 3 minutos. El puente se enrolla cada viernes al mediodía. En 2005 consiguió el premio de construcción Structural Steel Design Award. Sin duda: insólito y fantástico. AMJ
118 demostraciones del Teorema de Pitágoras.
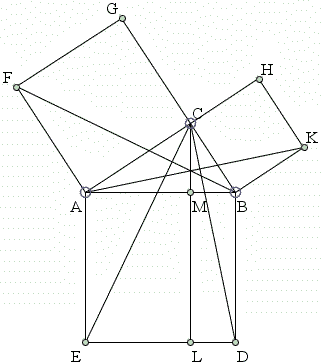
En este enlace http://www.cut-the-knot.org/pythagoras/ podemos ver 118 demostraciones del Teorema de Pitágoras, distintas evidentemente, desde la del Presidente de EEUU Garfield(en 1876) a la de Euclides (VI,31) o desde la Dudeney(1917) a la de Tao Tong(1994). Muy interesante. AMJ
Curiosidad de las milésimas de segundo.
Hay exactamente 1¹ × 2² × 3³ × 4⁴ × 5⁵ milisegundos en 1 día. AMJ
El tiro libre perfecto.
La distancia que necesita para encestar un tiro libre perfecto, dado el ángulo de elevación y la velocidad inicial del balón. AMJ
Los métodos de agotamiento y compresión de Arquímedes.
Arquímedes utilizó el método de agotamiento, inscribiendo polígonos regulares en una circunferencia de radio unitario para calcular su longitud, y además tal como aparece en este GIF, el valor aproximado de Pi. También utilizó el método de compresión, que al aumentar el número de lados de los polígonos, las figuras tenderán a acercarse a la forma de la circunferencia, tanto que Arquímedes pudo obtener una medida bastante precisa del número π. AMJ
El asombroso número 193.939.
Cambiando los dígitos con una permutación cíclica, los números resultantes son primos. ¡Asombroso! AMJ
El reloj dominó.
Vistiendo Matemáticas.
La teselación rómbica por todos lados. AMJ
¡Qué sería de una vida sin curvas!
Puerto de las Palomas. Grazalema.(Foto: duncan c en Flickr) AMJ
Diseño con ¡sólo círculos!
Sólo círculos. De @winstontabar AMJ
Reloj basado en la sucesión de Fibonacci.
(De antonio lozano,@cord7oba) AMJ