De extraordinario se puede calificar el documento publicado en la Gaceta de la RSME(Real Sociedad Matemática Española) en el Volumen 16, núm.3 titulado Sobre problemas de matemáticas en el estudio del cante flamenco, de José Miguel Díaz Báñez . Su autor es Profesor del Departamento de Matemática Aplicada II de la Universidad de Sevilla y desde 2004 aplica la ciencia matemática al mundo del cante flamenco, en lo que denomina “Teoría Computacional del Flamenco”, dirige cursos de Doctorado “interdisciplinando” ambas materias e imparte cursos sobre estas especialidades y sus relaciones. En este trabajo –que resumiremos- y que pueden enlazar aquí: personal.us.es/dbanez/flamenco trata de la búsqueda de propiedades de preferencia para los aficionados al flamenco, el cálculo de similitud musical y la simplificación de melodías. Todo ello posibilitará entender mejor la música flamenca y servirá como ejemplo de conceptos matemáticos básicos. Los temas que analiza en el artículo son: a) Un breve apunte de los cantes flamencos, b) Representación geométrica de ritmo y melodía, c) Ritmos regulares. Problemas de optimización, d) Medidas matemáticas de similitud. Comparando dos cantes flamencos, e) Aproximación de funciones. Simplificación melódica, f) Algunas reflexiones.
Los problemas que se plantean en este estudio profundizarán en el conocimiento de la música flamenca: problemas de matemática discreta y computacional –ya aparecidos en el COFLA (Análisis Computacional de la música flamenca)-. Las matemáticas, tan importantes en todos los campos, en la música también son útiles e igualmente, en la música flamenca. Se usan para detectar plagios, para identificar tipos de música, etc. El flamenco ha sido declarado “Patrimonio inmaterial de la Humanidad” y es objeto de estudio desde todos los ámbitos y perspectivas. Nuestro colega, el profesor Díaz Báñez, lo hace desde las matemáticas, estudiando características, singularidades y originalidad.
Comienza analizando los cantes flamencos, de tradición oral y, por lo tanto, peculiares, en comparación con la música clásica y presenta características independientes de cualquier otro tipo de música. Los aspectos fundamentales que estudia son el compás, la ornamentación y la improvisación; y sobre ritmo y melodía.
En las figuras siguientes vemos los cinco patrones rítmicos en 12 tiempos o en notación numérica:
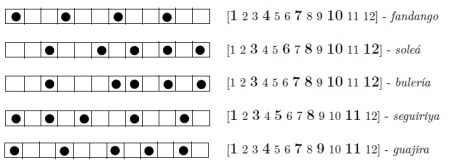
Continuamos con la Representación geométrica de ritmo y melodía.Se trata de codificar los parámetros musicales que se desean estudiar. Vemos la representación cronotónica – a base de histogramas-:
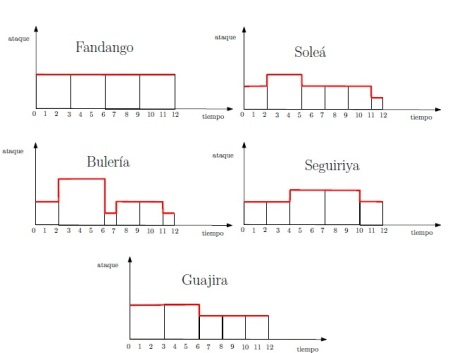
O la representación poligonal de los cinco compases del flamenco:
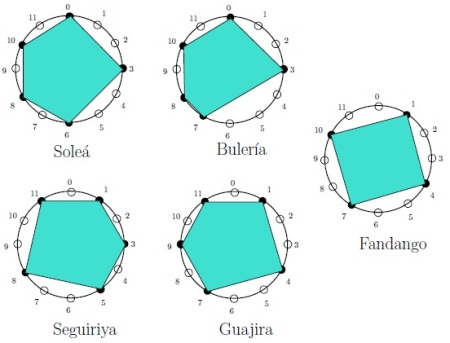
La melodía es el parámetro determinante en una canción, y se define de forma discreta –continua para audio- como una sucesión de frecuencias de sonido.
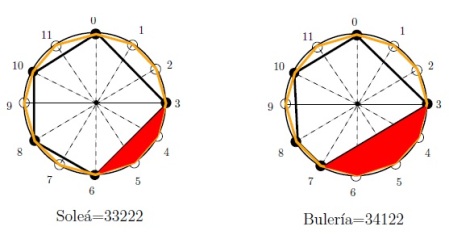
Y ahora van surgiendo los problemas matemáticos para observar la regularidad del ritmo, teniendo en cuenta el área del polígono rítmica:

Problema que introduce conceptos combinatorios y geometría.

Como podemos ver la soleá tiene más área que la bulería.

El artículo continúa con la Comparación de cantes flamencos, introduciendo medidas matemáticas de similitud, para ver el origen y evolución de distintos cantes flamencos. Para ello utiliza dos medidas: la distancia protónica y la distancia de permutación. En este gráfico podemos ver la distancia de permutación: un intercambio es válido para cambiar el compás.
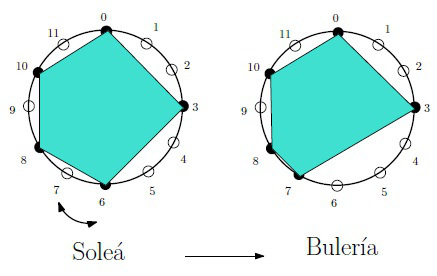
Los problemas 4, 5 y 6 sobre el cálculo de la distancia de permutación, la similitud melódica y el cálculo de la distancia de edición.



Continúa ahora con la simplificación melódica, para obtener la melodía principal del cante- no los adornos- y no depender de cada cantaor .Un grafo de similitud para cantes a capela sería:

Para terminar lo hace con dos problemas sobre funciones escalonadas y con el propósito de ampliarlos en estudios posteriores para buscar patrones musicales y poder clasificar cantes, estilos, distintas variantes de un mismo palo, etc.
El avance que supone este estudio es incuestionable, siendo muy útil para proyectos de investigación musical y de la aplicación de la tecnología a este campo: para reconocer canciones, autores, clasificar estilos,…

Desde aquí la enhorabuena por el avance científico conseguido, que aplicado a una música que se ha mantenido marginal a lo largo de los años, ha hecho del flamenco una música reconocible, más comprensible, menos anárquica, y en definitiva, maravillosa. El profesor Díaz Báñez podrá sentirse, ante el mundo flamenco y matemático, orgulloso de su estudio y desde aquí le agradecemos su dedicación y esfuerzo a estas materias.
La precisión, la minuciosidad, el talento, la dedicación, la exactitud y el rigor expuestos, sólo pueden provenir de un amante y estudioso de las dos materias: la mente prodigiosa de un científico que ha puesto en manos del público unos resultados que elevan a esta música a lo más alto. Lo dicho: enhorabuena, y en los enlaces del comienzo pueden ver el artículo en su totalidad- nosotros hemos hecho un pequeño resumen-. Noticias sobre este evento en ABC, agenciasinc.es y en la fundacióndescubre . Entrevista con el autor en El Correo de Andalucía.
Se lo decimos muchas veces: hay matemáticas por todos lados. Sólo hay que buscarlas. AMJ