Matemáticas y Geometría en la Naturaleza-II-(2015-->)

La rodocrosita, romboedros obtusos en la Naturaleza.

La rodocrosita es un mineral poco abundante, un carbonato de manganeso (MnCO₃) de dureza 4 (en la escala d e1 a 10). En su forma pura, tiene un característico color rosa rojizo, si bien es poco frecuente encontrarlo así. En función de las impurezas, la tonalidad de este mineral puede variar desde el rosa hasta el marrón claro.

 Las formas cristalizadas, poco frecuentes, son romboedros obtusos cuyo ángulo suele ser de 107º 20’ con doble refracción, de 3 a 5 milímetros; a veces sus caras son curvas presentando forma lenticular muy marcada. Debe su nombre a su característico color (del griego ῥόδον, ródon, color rosa). Es la Piedra Nacional Argentina.

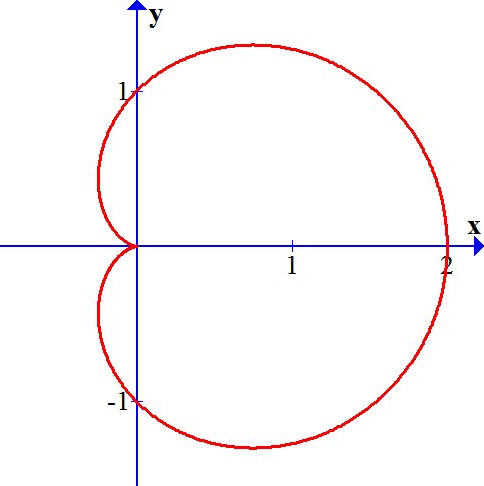
Su aspecto geométrico es impecable; de ahí,  la perfección en la Naturaleza. AMJ

Columnas hexagonales en la desecación del almidón de maíz.

Experimentos realizados con  almidón de maíz, conocido aquí en España como Maizena, prueban que la desecación de este material produce unas columnas como las producidas por el basalto, ya estudiadas en este blog (En Geometría y Naturaleza en  La Calzada del Gigante en Irlanda). Las columnas poliédricas hexagonales -prismas- suelen ser irregulares, pero algunas de ellas son totalmente regulares, como pueden apreciar en la fotografía. Este patrón ya fue observado en el siglo XIX por Huxley.En la imagen inferior pueden ver la disyunción en las columnas de basalto(a la izquierda) y las del almidón(Drcha):

                     

Las Matemáticas están ahí. Sólo hay que buscarlas. AMJ

El cardo esférico y la esfera -Echinos ruthenicus-.

Una esfera especial la de este cardo, el echinos ruthenicus. Preciosa. (foto: Tecnoe en Flickr). AMJ

La espiral de Fibonacci y el huevo.

Probando la espiral de Fibonacci y la fotografía de un huevo, James Milstid comprobó que "coincidían" a la perfección. Sólo tuvo que colocarlas. Esa espiral, que tanto vemos en la Naturaleza, la vemos hoy en Flickr, gracias a nuestro amigo James. AMJ

¡¡El caracol arcoiris: una espiral bellísima!!

El Polymita picta -polymita, en griego: muchas rayas; y picta, en latín: pintado- es un caracol endémico de la isla de Cuba, particularmente de Baracoa, de donde es su símbolo. Su espiral la lleva decorada con una variedad insultante de colores. Belleza y geometría: ¡¡nuestra espiral , algunas veces, es que se pone irresistible!! AMJ

(De P.Eimon en Flickr)

La geometría íntima de la naturaleza en Doñana.

Parece arte moderno o exquisito arte geométrico; pero nos equivocamos. Se trata de una serie de fotografías que ha realizado desde el aire Héctor Garrido y que expone en el Palacio de la Moncloa, sede de la Presidencia del Gobierno de España, bajo el título  Fractales. Las marismas y Doñana. Según su autor es  “una invitación a comprender como funciona nuestro planeta y propiciar el respeto que se merece”. Vean reseña en El País. AMJ

Escultura -curva- natural.

.

 Semillas de geranium sanguineum.(Fotos de flips99 en Flickr).  AMJ

El jengibre(Zingiber) y sus inflorescencias geométricas.

El jengibre (Zingiber officinale) es una planta de la familia de las zingiberáceas, conocida por su tallo subterráneo o rizoma, apreciado por su aroma y sabor picante, y cómo no, por sus propiedades terapéuticas.  Se utiliza para elaborar caramelos, pan, bebidas,… y en medicina para tratar las náuseas o incluso Avicena lo utilizaba como afrodisíaco. Las raíces son fibrosas y secas, pero nosotros lo traemos aquí por sus flores  y su fruto. La inflorescencia forma parte de un tratado geométrico profundo; con un patrón raro pero milimétrico y el fruto es una cápsula parecida a un elipsoide. Las fotos que les dejamos atestiguan la belleza de Naturaleza, Color y Geometría. AMJ

Geometría de la datura: espirales fantásticas.

La datura es una planta herbácea perteneciente a la familia de las Solanáceas. Su nombre viene de su fruto: “manzana espinosa”.Nosotros lo traemos por aquí por sus flores y sus frutos. Por la espiral que forma la flor antes de abrirse, que en algunos casos es de una perfección asombrosa. AMJ

Physalis Alkekengi -el Alquejenje o farolillo chino-: la esfera escarlata.

	P.Peruviana

El Alquejenje o farolillo chino –Physalis alkegengi- es una planta de la familia de las solanáceas –al igual que la patata, el tomate o el tabaco-  que se cultiva en los lugares cálidos de casi todo el mundo.  El fruto es una baya de color rojo escarlata -¡¡una preciosa esfera!!- envuelta en una vesícula que diríamos “fractal”. A lo largo de la historia ha sido comestible, pero ahora se desaconseja. Otra variedad de la Physalis, la peruviana,    procede de Perú -le llaman también "el bombón andino-, con bayas amarillas y con propiedades medicinales amplísimas.

 La geometría y la belleza vuelven a estar unidas, nuevamente, en la Naturaleza. AMJ

Tritoniosis elegans, fractal natural.

Los nudibranquios -con las branquias al desnudo- son moluscos gasterópodos, de los que traemos hoy el Tritoniopsis elegans, un especimen bastante raro, de unos 5 cms. que habita en el Índico y el Pacífico. Como vemos es un ejemplo claro de fractal natural. Precioso. AMJ

Geometría poligonal del hongo Clathrus ruber.

No. No está preparado. El hongo Clathrus ruber es así de esbelto. Ayudado por la Geometría presenta este aspecto impresionante.

Sale de esta especie de huevo, desde el suelo:

A ciencia cierta, no se sabe si es comestible o no; pero fétido sí que es. El Clathrus ruber , conocido también como "jaula roja" es una especie saprófita, con un olor a "carne en descomposición" que atrae a moscas y otros insectos, que le ayudan a la reproducción, dispersando las esporas. En algunos casos, la malla roja o naranja que le rodea presenta polígonos -pentágonos o hexágonos- cuasiregulares .Se puede encontrar en España y en zonas del norte de América, entre otros lugares. Todo un portento geométrico que nos ofrece la Naturaleza. AMJ

Orden y geometría.

Animales que construyen sus casas como si de arquitectos se trataran. El orden y la geometría imperan en sus construcciones. Entre ellas las perfectas y simétricas -casi todas- construcciones de las arañas ¡De ellas tenemos que seguir aprendiendo! Extraordinario documental de La 2 de TVE.  AMJ

La perfección geométrica de la flor de la lantana.

(De M.Greenjeans en Flickr)

(love.rose en Flickr)

(M. Schdmit en Flickr)

(I.Pillai en Flickr)

(Ilaw en Flickr)

Las lantanas son un género de plantas de la familia de las Verbenaceae, con más de un centenar de especies,  en su mayoría de América. Aquí en España, cuyo clima le es propicio, se les suele llamar Verbena o “Banderita de España”, por los colores amarillo y rojo de sus flores. Suele haberlas de colores variados, pero predominan las rojas, amarillas o mezcladas. Las hojas y sus frutos son tóxicos, aunque en infusiones tiene distintas propiedades terapéuticas. Su inflorescencia en corimbos nos hace que la traigamos por aquí: presenta unas regularidades maravillosas, círculos concéntricos simétricos y, para cuando está totalmente abierta es una semiesfera espectacular,  tal como se aprecian en estas imágenes que les hemos traído. AMJ 

(E.Odegard en Flickr)

(De C.V. Prince en Flickr)

Scabiosa Stellata, perfección geométrica.

(De J.E.Monje en Flickr)

(J.C.Poveda en Flickr)

La Scabiosa Stellata, llamada por aquí Farolitos; es una planta de la familia de las madreselvas, que crece en el Sur de Europa y África del Norte, en campos abandonados y bordes de caminos. Los frutos están en el centro de un paraguas, formando una esfera. La traemos por aquí por esta bella geometría que nos presenta en las flores: una estrella de cinco puntas curvilínea. Preciosa. AMJ

El corazón simétrico de la amapola.

(Mary Maa en Flickr)	(C Rebull en Flickr)
(C Rebull en Flickr)	(A. Lafond en Flickr)

(D. Rocal en Flickr)

La amapola   es una planta angiosperma, conocida también como papaver, que se distribuye por todo el hemisferio Norte y que alegra los campos con su color rojo intenso –también las hay de otros colores-. Hay más de 400 especies descritas, pero nosotros la traemos por aquí por su interior. Cuando se le empiezan a caer los pétalos comenzamos  a vislumbrar la simetría que presenta. El coeur de coquelicot, o corazón de la amapola presenta  de 6 a 10 discos y en otros casos hasta 12 y más  –meridianos-, perfectamente simétricos. Toda una preciosidad que estaba escondida bajo la belleza de la flor. AMJ

¡¡¡Y esta de 13 radios!!!(De Kimhaz en Flickr)

Geometría espinosa o ¿fractal?

(De Sánchez Mesa en Flickr). De este fotógrafo de Algodonales(Cádiz), este cactus esférico que es un auténtico fractal. AMJ

La lechuza y la función r=1+cos(θ).

La función es r=1+cos(θ), con 0≤θ≤2π

¡Para que luego me digan que no hay relación entre las Matemáticas y la Naturaleza!. La función que le traemos -en coordenadas polares-  si la giramos 90º nos aparece la cara de este fantástico animal: la lechuza -habitante de estos lugares de España-. (La idea de @pickover) AMJ

Sistemas cristalinos(I): Hexagonal.

Un mineral es una sustancia natural inorgánica, con una estructura atómica definida de elementos químicos y si se ha desarrollado bajo unas condiciones ideales –sin impedimentos-, entonces presenta  patrones geométricos- unos más conocidos que otros-. A esa formación se le lama cristal. Las condiciones ideales que hemos mencionado suelen ser: temperatura, presión, espacio, tiempo,.. La cristalografía es la ciencia que estudia las estructuras cristalinas, y la clasificación  se interpreta según las propiedades de simetría: centro, ejes y planos de simetría. Se agrupan en 7 sistemas, que son el cúbico, tetragonal, romboédrico o trigonal, rómbico, monoclínico, triclínico  y hexagonal.

Vanadinita:Prismas brillantes de diferentes colores. Composición:Clorovanadato de plomo.	Aguamarine.
Berilo. Composición:Ciclosilicato de berilio y Aluminio.	Vanadinita Bazzita.

 Hoy vamos a traer el sistema hexagonal. Tiene la misma simetría que un prisma regular de base hexagonal, tiene siete planos de simetría, un eje senario y un eje binario. La sformas que presentan pueden ser: el prisma hexagonal, la pirámide hexagonal y el prisma y la pirámide dihexagonal. Entre ellos están  el berilo, el grafito, la vanadinita,el agua cuando se solidifica, etc.(Ver más en Wikipedia)

Consta de cuatro ejes cristalográficos, de los cuales tres son horizontales e iguales entre sí. El cuarto eje (z) -vertical- es mayor a los anteriores  (x=y=x´1≠z). Los ángulos verticales -Alfa, Beta  y Delta- miden 90°.  El ángulo horizontal -Gamma- es de 120°.

Nosotros traemos este estudio aquí para ver que la Geometría y la Naturaleza van íntimamente relacionadas. Las imágenes que les traemos nos prueban que las Matemáticas están ahí: sólo hay que buscarlas.AMJ

(Greennockita)

(Zemmanita)

La granada, geometría desde la antigüedad.

El granado, o punica granatum, es un arbusto de hoja caduca cuya fruta es la granada (pomegranate), cuyo origen va desde los Balcanes hasta el Himalaya. Lo traemos por aquí porque observando tanto la flor como el fruto le encontramos una geometría perfecta. Es cierto que algunas variedades las maravillas geométricas no son regulares ni perfectas, pero en otras, la perfección es su patrón de crecimiento.

Las flores, solitarias, hermafroditas, de cáliz campaniforme de segmentos triangulares soldados y persistentes en el fruto, y que suelen ser de 5 a 8, como los que vemos en las imágenes siguientes:

El fruto, la granada, es esférico, coronado por los  segmentos del cáliz, que contienen las semillas granates comestibles, que a veces, cuando tomamos una imagen de la granada cortada transversalmente vemos estos sectores circulares similares que conforman el fruto, dependiendo su número de sus segmentos triangulares:

Desde la antigüedad se le ha asociado con la fecundidad  por las culturas judía y cristiana, e igualmente  por las culturas griega, romana, china,…. y no digamos sus propiedades medicinales como antioxidante: algunas de ellas son formidables. Los bereberes la traen hasta Granada en el siglo X, y de ahí su nombre. Está en el escudo de  España. E incluso ¡las hay negras!.

Una vez más, la unión de Geometría y Naturaleza nos dan belleza y perfección. AMJ

Detalle de Virgen de la Granada de Boticelli

También las pintaron  españoles:

Zurbarán

Andrés Cortés y Aguilar(1812-1879)