La geometría barroca de Leonardo Sinisgalli(1908-1981), un renacentista en el siglo XX.

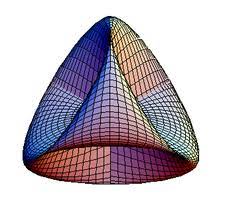





Teníamos aquí, en Matemolivares, el heptágono equilátero curvo, la moneda de 50 peniques del reino Unido.
Hoy les traemos otra igual de bella y geométrica. La moneda de 50 peniques con la misma forma geométrica y con la explicación del "fuera de juego" en el fútbol. Así que ya saben, aficionados en tiempos de Eurocopa, cuándo dudéis si es fuera de juego o no, tengan la moneda de 50 peniques a mano, con el logotipo de los Juegos Olímpicos de Londres 2012 arriba y la denominación “50 PENCE” debajo,diseñada por Neil Wolfson. AMJ


Alfonso X, el Sabio, accedió al trono de Castilla y León en 1252, a la edad de 30 años. Escribió bastantes obras(“Estoria de España), Tablas Alfonsíes, Las Siete Partidas,….), y entre ellas nos hemos fijado en el “Libro de los Juegos”, donde aparece el juego “Juego de Tablas Astronómicas”, una variante a siete del Backgammon. Representa el movimiento de siete cuerpos celestiales sobre las estrellas. Cada jugador representa un planeta y sus fichas están dibujadas acorde con el color de cada planeta: Saturno-negro, Júpiter-verde, Marte-rojo, Sol-amarillo, Venus-violeta, Mercurio-policromo, Luna-blanca. Las reglas del juego pueden verla en laficharoja.com
Pero nosotros lo hemos traído por aquí al observar el heptágono regular que forma el panel del juego. Algo no muy usual en aquel tiempo (finales del siglo XIII). (Una copia de 1334 se conserva en la biblioteca de la Real Academia de la Historia.
Todo un lujo: geometría y teoría de juegos: ¡¡Matemáticas al poder!! ¡¡Ay si los reyes de ahora se dedicaran a estas cosas!! AMJ
Pierre Hérigone (latinizado como Petrus Herigonius) (1580-1643) fue un matemático y astrónomo francés. Destacó por el uso sistemático de terminología y de símbolos matemáticos novedosos en sus tratados. De origen vasco(del País Vasco francés), Hérigone enseñó en París durante la mayor parte de su vida.
Solo se conserva uno de los trabajos Hérigone: Cursus mathematicus, nova, brevi, et clara methodo demonstratus, per notas reales et universales, citra usum cujuscunque idiomatis intellectu faciles (publicado en París en seis volúmenes de 1634 a 1637; segunda edición de 1644), un compendio de matemática elemental escrito en francés y en latín, casi por completo en símbolos, en el que propuso por primera vez el uso de ⊥ (perpendicular) y ∠ (ángulo).
El objetivo de Hérigone era crear un lenguaje simbólico como lenguaje universal para tratar las matemáticas. Estos son algunos de los otros símbolos que intentó introducir en su libro.
Algebra in the Cursus mathematicus (París, 1634, 1637 , 1642; segunda edición 1644) por Pierre Hérigone (1580-1643).
Hérigone fue uno de los primeros matemáticos en considerar que el lenguaje simbólico podría usarse como un lenguaje universal para tratar las matemáticas puras y mixtas. Mostramos que, aunque Hérigone generalmente usaba las declaraciones de Viète, su notación, estilo de presentación y procedimientos en sus pruebas algebraicas eran bastante diferentes de las de Viète. Además, enfatizamos cómo Hérigone manejó las operaciones algebraicas y los procedimientos geométricos haciendo uso de proposiciones de los Elementos de Euclides formulados en lenguaje simbólico.
(Para saber más, ver sciencedirect.com ) ¡¡Fantástico!! AMJ

(Estos 6 tomos se encuentran en la Biblioteca de la Un. de la Sorbona).

Parece raro, pero es cierto. En los tiempos de las “fake news” por doquier, ésta que les traemos hoy es cierta. Vamos a explicarla.
Hasta ese día, 4 de Octubre, el calendario que imperaba era el Juliano, instaurado por Julio César en el año 46 a.C. El sistema calculaba que los años terrestres duraban 365 días y seis horas (divididos en 12 meses), e incluía un día más cada cuatro años.

Es decir, igual que ahora, había un año bisiesto cada cuatro años. El problema surgía porque contaba más tiempo del debido. En realidad el año tiene 365 días, 5 horas, 48 minutos y 45,25 segundos; es decir el año juliano duraba aproximadamente 11 minutos y 14 segundos más. Haciendo cálculos la humanidad se atrasaba alrededor de un día cada unos 130 años. Por lo tanto el desfase iba siendo más grande, de tal manera que al llegar al siglo XVI, había cerca de 10 días entre las fechas y las estaciones de la Tierra y las fiestas religiosas, como la Pascua (Semana Santa), que iban cayendo cada vez más temprano.
En 1572 llega a Roma el Papa Gregorio XIII y decidió resolver la cuestión. Encargó a C. Clavius un nuevo calendario. La principal dificultad la soslayó de la siguiente manera: el nuevo sistema modificó la regla de los años bisiestos. Estos se mantuvieron cada cuatro años, pero con dos excepciones.

Se decidió que los años que fueran múltiplos de 100 no serían bisiestos, pero los que fueran divisibles por 400 (por ejemplo 1600, 2000, 2400) lo seguirían siendo. El error parecía casi resuelto, a excepción de que el sistema erraba alrededor de medio minuto por año, es decir 1 día cada 3.300 años. Para arreglar el desfase que había con respecto al equinoccio de primavera, que ya lo llevaban por el 11 de Marzo, se dispuso que fuese el 21 de Marzo y para lograrlo en los siguientes años, el edicto ordenaba que ese mismo año, el 1582, el calendario pasara del jueves 4 de octubre al viernes 15 de octubre.

Así, los días del 5 al 14 de octubre de 1582 no existieron. Los territorios que corresponden actualmente a Italia, España y Portugal fueron los primeros en adoptar el cambio. Poco a poco el resto de países occidentales fueron adoptando el nuevo calendario, llamado desde entonces calendario gregoriano. Como anécdotas terminaremos contando que Santa Teresa de Jesús murió el jueves 4 de Octubre de 1582 y enterrada al día siguiente viernes 15 de Octubre de 1582.
Desde entonces nuestro calendario goza de buena salud. AMJ

Isaac Newton nació -el día de Navidad de 1642- en la aldea de Colsterworth en Lincolnshire, cerca de Grantham, una ciudad del este de Inglaterra. Anécdotas de esta ciudad recordamos que en ella nació la primera ministra del Reino Unido Margaret Thatcher y que tine la torre de una iglesia más alta de Inglaterra y la biblioteca pública más antigua del país, fundada en 1598. El Colegio donde estudió Newton todavía sigue en pie y funcionando.
Pero nosostros henos traído esta imagen porque Isaac Newton, evidentemente, también fue niño y una de sus travesuras fue dejar este reloj de sol con sólo nueve años, tallado en piedra con una navaja en la iglesia de St. John's donde se bautizó el día Año Nuevo de 1643 . ¡Era travieso, pero qué travesuras se le ocurrían! AMJ

Un mapa de ahora, con tosdo tipo de herramientas:

Ahora tenemos GPS, satélites, todo tipo de herramientas de medida, todas ellas muy sofisticadas, pero 1400 años a.C. también tenían algo: cerebro, y les sirvió para fabricar en arcilla esta tablilla con el plano de Nippur(Irak) bastante asemejado a la realidad. AMJ

Al parecer la primera persona en dibujar la Luna, tal como se ve a través de un telescopio, no fue Galileo Galilei sino Thomas Harriot (1560,1621), un matemático británico -creador entre otros símbolos algebraicos > y > -. Así se corrobora en una exposición que se inaugurará el 19 de Julio en el Royal Museums Greenwich. Ver más en National Geographic) AMJ

La versión digital pueden consultarla completa aquí: Principia AMJ
Al- Mayriti (Âbû-l-Qâsim Maslama ibn Âhmad al-Faradi al-Hasib al-Qurtubî al-Maŷrîtî) nació en el año 950, en Madrid.Como todos los jóvenes de los pueblos, tuvo que emigrar. Sí, Madrid era un pueblo y de los pequeños, fundado en la segunda mitad del siglo IX, por el emir de Córdoba Muhammad I. En los tiempos que no había censo era difícil precisar los habitantes de cada uno de ellos pero Madrid no llegó a los 3000 habitantes hasta el año 1300 aproximadamente; y entonces ¿dónde fue nuestro joven Muslama? A la ciudad más avanzada y poblada , la capital de Occidente, donde científicos, literatos, traductores, matemáticos, médicos, … poblaban una ciudad, que en algunas crónicas de historia le dan una población cercana al millón de habitantes, de unos 4 millones que tenía España en aquel momento. Era Córdoba, donde se almacenaba el saber del primer milenio.

A Córdoba se fue nuestro joven y como el talento no es exclusivo de las grandes ciudades, rápidamente se incorporó al estudio de las Matemáticas, la Astronomía y la Astrología; donde fue discípulo del geómetra ‘Abd al-Gâfir ibn Muhammad. Su estancia en Córdoba coincidió con uno de los momentos de mayor esplendor cultural de la civilización hispano-árabe, con la residencia de Madinat al-Zahara (cuyas academias y sociedades culturales eran frecuentadas por los principales eruditos e investigadores de la Baja Edad Media) convertida en un importantísimo centro del saber mundial; donde el conocimiento se organizó en torno a dos grupos fundamentales: el Astronómico-Matemático, cuyo principal exponente fue Maslama, y el Físico-Botánico-Médico, en torno al cordobés Abulcasis, precursor de los no muy posteriores Averroes y Maimónides.

Dicen de él: “..fue el científico más importante de su tiempo en el mundo islámico y en la Europa cristiana, puesto que sus libros se tradujeron al latín muy rápidamente”. Fue un gran astrónomo, resumió y comentó la obra del matemático oriental Al-Juarismi y tradujo y perfeccionó el Astrolabio y el Planisferio de Ptolomeo; convirtió el calendario persa a las fechas árabes empleando la Hégira como punto de partida para el cálculo. Fue el consejero astrológico de Almanzor, indicando los momentos oportunos en que debía empezar sus campañas, y se dice que pronosticó el fin del Califato y los detalles de cómo iba a ocurrir mucho antes de que tales hechos pasaran.
Entre sus obras destacan: "Tratado del Astrolabio", Tablas Astronómicas, "Libro de Aritmética Práctica", "Rutbat al-hakim" ("La Distinción del Sabio"), "Ghayat al-hakim" ("El Acierto del Sabio") y tratados de aritmética comercial ("Fi taman ilm al-adad", "Teoría de la perfección de las ciencias numerales", y "al-Mu’amalat", "Cálculo comercial"). (Para más profundidad, ver elmadridmedieval)
Maslama fundó en Madrid una Escuela de Matemáticas y Astronomía, documentada en el año 1004 y murió en Córdoba en el 1008.

A que se debe la falta de reconocimiento de este científico madrileño en su tierra natal. Para algunos historiadores del mundo árabe, Al-Ándalus es circunscrita casi exclusivamente a Andalucía y fuera de esos territorios cualquier personaje notable queda fuera del cuadro de honor de la historia. Y eso ocurrió con Al Mayriti, El Madrileño, nadie lo reivindicó y en el olvido de la historia ha quedado; sin embargo para otros estuvo a la altura de otros premios Nobel españoles, como Severo Ochoa o Ramón y Cajal. AMJ


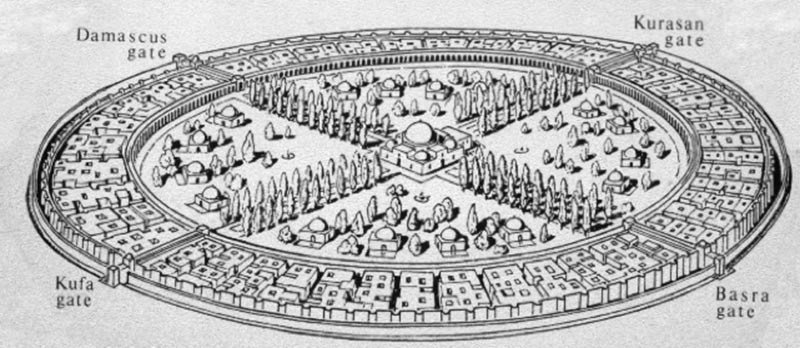
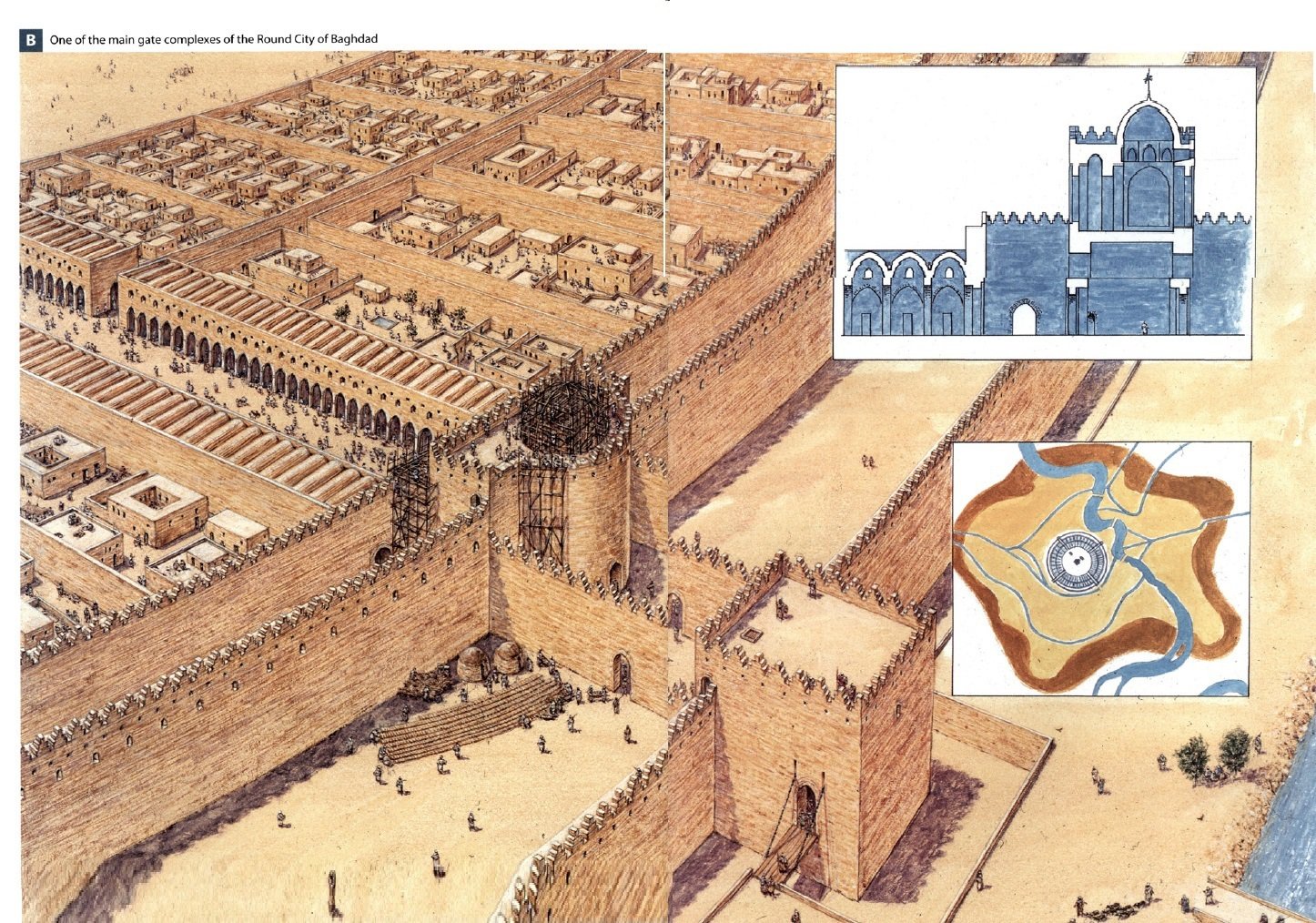
En el año 761 Al-Mansur (el Victorioso) fundó Bagdad, cerca de las ruinas de la antigua Babilonia y la convirtió en la capital del islam; la llamó Madinat-al- Salaam. Mansur creía que Bagdad era la ciudad perfecta para ser capital del imperio islámico bajo el Califato Abasí. En el año 758, Mansur reunió ingenieros, agrimensores y artistas de todo el mundo para elaborar planes para la ciudad. Más de 100.000 trabajadores participaron en la construcción, que comenzó el 23 de julio del año 762 d. C.
La ciudad fue diseñada como un círculo de 2,7 kilómetros de diámetro. El diseño original mostraba un anillo de viviendas y estructuras comerciales a lo largo de la parte interior de los muros de la ciudad, pero la composición final añadió otro anillo, dentro de la primera. En el centro de la ciudad se situó la mezquita, así como el cuartel de la guardia. El diseño circular de la ciudad es una idea tradicional persa Sasánida: avenidas radiales y edificios del gobierno y templos en el centro de la ciudad. Se utilizó mármol para hacer los edificios, se construyeron muchos parques, jardines, villas y bellos paseos que daban a la ciudad un elegante acabado.
Era una ciudad amurallada, con cuatro puertas, rodeada por un foso. El muro era de aproximadamente de 44 m de ancho en la base y unos 12 metros en la parte superior, y de unos 30 m de altura, incluyendo las almenas. Este muro estaba rodeado por otro impresionante muro de un espesor de 50 m( es decir, una doble muralla). En el centro de la ciudad se situó la mezquita, así como el cuartel de la guardia.
Era el Bagdad de Las mil y una noches, de los zocos, las mezquitas, los palacios, las bellas princesas árabes, los comerciantes que remontaban el Tigris trayendo todo tipo de productos, de las sederías y las alfombras. Una parte de la población de Bagdad no era árabe, y había pobladores persas, arameos y griegos, pero estas comunidades adoptaron progresivamente la lengua árabe.
En el National Museum of American History (Smithsonian), se expone la servilleta en la que Art Laffer, economista de la Escuela de Chicago, les explica -allá por 1974- a dos asesores del presidente Gerald Ford la curva en la que aloja una teoría revolucionaria: bajar los impuestos aumenta la recaudación fiscal.
El tiempo ha demostrado que no era cierta. Sólo lo es en los extremos: si el tipo del impuesto es cero se recauda cero y si el tipo del impuesto es el 100%, también se recauda cero, porque nadie trabajaría si el Estado se quedara con el 100% del rendimiento. ¿Pero qué pasa dentro de la curva? El tiempo ha puesto a la curva en su sitio. (ver más en diario.es ).

La curva muestra en abscisas los tipos impositivos posibles (t) y en ordenadas la recaudación fiscal (T) que se consigue a ese tipo impositivo. El máximo aparece en el centro por cuestiones de claridad, en una curva real podría estar desplazado a la derecha o a la izquierda. Aunque más posiblemente a la derecha. El problema es que nunca sabemos si estamos a la izquierda o a la derecha del máximo, La ideología imperante en los últimos años nos hace ver que estamos siempre a la derecha del máximo( de la máxima recaudación) con lo cual si disminuimos los impuestos aumentaríamos la recaudación, pero ¿quién sabe dónde estamos en cada momento? Ejemplos hay para todos los gustos, por lo tanto lo dífícil es saber la posición momentánea: no siempre es la misma, aunque algunos intenten convencernos -con publicidad, propaganda,... - que eso es lo mejor para todos. Ya sabemos que no siempre, pero para ellos siempre es mejor disminuir los impuestos. Dicho queda. (Ver más interesantes en wikipedia y enlaces ). AMJ

Algunos sostienen la idea de por qué ha sido olvidada, simplemente diciendo que "ella es una mujer y no tenía un" esposo "famoso", lo que podría ser el caso. Se sabe muy poco acerca de ella, principalmente porque hay muy pocas fuentes sobre esta mujer notable, y la credibilidad de estas fuentes a menudo puede ser cuestionada. A pesar de estos contratiempos, vale la pena mencionar las cosas que se conocen, porque es importante que la gente recuerde su nombre.

(Medina Azahara, Córdoba).
Algunos dicen que Lubna nació como una esclava española -no se conoce su fecha de nacimiento, pero vivió en la segunda mitad del siglo X-, lo que la hace llegar a la fama y el privilegio en la corte andaluza aún más notable. Durante su vida, Lubna se convirtió en una de las figuras más importantes de la corte andaluza, primero como secretaria y escriba, y más tarde como secretaria personal del hijo de Abd Al-Rahman, Hakam II Ibn Abdur-Rahman (Alhakén II).
Córdoba en aquel tiempo era avanzada en tecnología, innovación científica y recursos, en comparación con sus homólogos europeos como París y Londres donde no había agua corriente, ni luces de la calle;contaba con más de 200.000 casas, 600 mezquitas con sus respectivas escuelas infantiles, 80 escuelas de enseñanza superior, 900 baños públicos y 50 hospicios.
Además de ser secretaria personal de Alhakén II se le encomendó presidir la biblioteca real de Córdoba, considerada como una de las bibliotecas más importantes de su tiempo - que en ese momento incluía 500 mil libros-, por lo que no fue una hazaña que se pusiera a cargo de ella una mujer(Ver más). Algunas fuentes afirman que ella era personalmente responsable de adquirir nuevos artículos para la biblioteca, y que viajó a El Cairo, Damasco y Bagdad para hacerlo. Su papel como escribiente era igualmente importante, ya que iba más allá de los deberes estándar de ser escritor y traductor. Fue responsable de la copia de muchos textos importantes, incluidas las obras de Euclides y Arquímedes, así como de proporcionar sus propias anotaciones a los textos ya existentes.También se decía que era una gran matemática, y hay fuentes que afirman que a menudo caminaba por las calles de Córdoba para enseñar ecuaciones matemáticas a los niños. La seguirían mientras recitaban las tablas de multiplicar que ella les había enseñado, hasta que llegaban a los muros del palacio, más allá del cual el acceso estaba restringido.

El historiador y cronista Ibn Bashkaval se refirió a ella de la siguiente manera: "Ella sobresalió en escritura, gramática y poesía. Su conocimiento de las matemáticas también era inmenso y también era competente en otras ciencias. No había ninguno en el palacio de los Omeyas tan noble como ella.Incluso yendo un poco más en profundidad, Algunos estudiosos del mundo islámico sugieren que la imagen que tenemos hoy de Lubna es en realidad la combinación de dos mujeres diferentes. Una de ellas era de hecho Lubna, mientras que la otra era posiblemente una mujer llamada Fátima. Argumentan que Lubna era efectivamente matemática, escriba, copista y poeta. Pero en realidad fue Fátima quien recorrió los mercados de libros del mundo árabe en busca de obras para agregar a la biblioteca real. La razón por la que estas dos mujeres se comprimieron en una sola identidad, borrando así a Fátima de la historia, fue porque el escritor responsable de esto encontró imposible comprender que podría haber dos intelectuales -¡¡ y mujeres!!- en la corte al mismo tiempo. O al menos esto es lo que consideran la explicación más lógica. Una mujer puede ser vista como una excepción, argumenta, pero la idea de que más de una mujer podría haber tenido éxito trae consigo un nuevo conjunto de expectativas sobre la cultura prevaleciente . Y esto, al menos para los cronistas e historiadores, fue más fácil de ignorar. Podría haber una multitud de intelectuales masculinos y nadie lo habría pensado dos veces, pero desafortunadamente, debido a su género, a estas dos mujeres no se les permitió coexistir en las páginas de la historia.

Lo que es sorprendente es que las mujeres como Lubna y Fátima no eran únicas en el momento del reinado de Hakam II, pero tampoco eran exactamente comunes. Karmila Shamsie, investigadora de origen paquistaní, dice, para la BBC, que había un punto intermedio entre las dos extremidades. En el siglo X en Al-Andalus había más académicas que eran hábiles matemáticas, poetas, lingüistas, etcétera . La razón por la que se sabe tan poco sobre ellas dice más sobre la cultura dominante de los historiadores y biógrafos que optaron por omitir a estas mujeres de sus cuentas, que sobre los contemporáneos de estas mujeres. Por eso, a pesar de las muchas incertidumbres e imprecisiones históricas, es necesario contar sus historias. Desconocida y olvidada, quizás desterrada del conocimiento de los andaluces y españoles, casi exclusivamente por el hecho de ser mujer. Desde aquí la reivindicamos en el día de Andalucía, 28 de Febrero, y en el Día de la Mujer Trabajadora del 8 de Marzo. AMJ



En la playa de Koekohe, en Moeraki (Nueva Zelanda) nos encontramos estas raras esferas, que al igual que ya trajimos aquí unas en Costa Rica (Las esferas de Costa Rica: geometría misteriosa, simple y maravillosa), éstas son igualmente misteriosas. Pueden tener de 0,5 metros a 2,2 metros de diámetro y pueden llegar a pesar hasta siete toneladas. Las rocas son producto de un fenómeno natural: son concentraciones cálcicas que se formaron hace unos 65 millones de años, en la época de los dinosaurios. Aunque están muy lejos, en las antípodas, merecen una visita. AMJ


William Hamilton, matemático irlandés que mientras un buen día paseaba por el Royal Canal de Dublín junto a su esposa, se le vino a la cabeza la regla de multiplicación de los cuaterniones. Para que no se le olvidase y a falta de papel y lápiz, cogió su cortaplumas y grabó dicha fórmula en una de las piedras del puente Broom Bridge, que como ven no es nada del otro mundo; pero por esa incripción quedó para la posteridad.

(Ver más en Talesofawanderer) AMJ
|
|
El cuboctaedro es uno de los sólidos arquimedianos, de catorce caras -8 triángulos equiláterosy 6 cuadrados-, un tetrakaidecaedro. Se obtiene truncando un cubo por cada uno de sus vértices. Lo hemos visto en muchos sitios por ahí: les traemos algunos:

Reloj de Sol poliédrico, con gnomon en trece de sus caras -se apoya en la cara nº 14 que es donde se apoya. Procede del Norte de Inglaterra, en Sunderland, alrededor de 1700, construido en piedra, deunos 85 cm de altura; en el Victorian and Albert Museum de Londres.
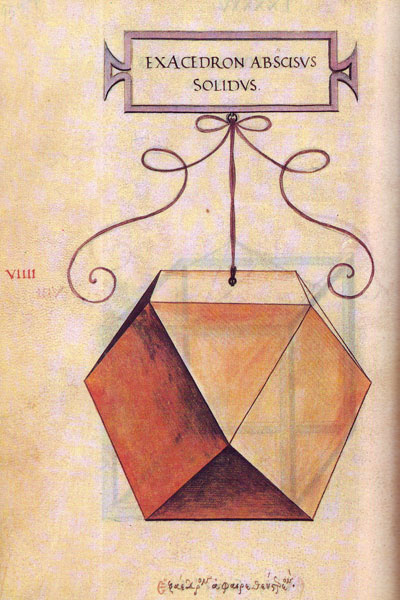
(Dibujo de Leonardo da Vinci para "La divina proporción" de Luca Paccioli.
 |
Dos cuboctaedros en las calles de Alemania(De Matemáticas visuales).

Cuboctaedro temporal construido en Nailsea, Inglaterra, en 1976.

En Lhasa, Tibet(China). Cuboctaedro en piedra, como adorno en una barandilla en palacio.

(En Chinatown, San Francisco).

Adornando una escalera. (Xiamen, China)
 |
 |
|
|
En este equipo de música (hecho en piel, a mano, en una edición de lujo), nuestro poliedro está presente en ¡todos sus elementos!

(Como mesa de diseño, Geo baby, en Homebasic)
|
|
|
(Las jardineras de Air Plant Holder)
¡¡Fantástico nuestro cuboctaedro!! AMJ
Sabíamos de la existencia del juego de dados en la antigua Roma(lo tenemos aquí recogido en Matemolivares: Juego de dados en el Imperio Romano), como una distracción del ejército romano cuando descansaban entre batalla y batalla. Ya está recogido en La Biblia el juego de azar entre los romanos:
San Juan 19.24. Entonces dijeron entre sí: No la partamos, sino echemos suertes sobre ella, a ver de quién será. Esto fue para que se cumpliese la Escritura, que dice:”Repartieron entre sí mis vestidos,Y sobre mi ropa echaron suertes”. Y así lo hicieron los soldados.
![[Imagen]](http://archive.archaeology.org/1105/world/images/pakistan.jpg)
Hoy les traemos estos mismos dados pero utilizados en otra cicilización mucho anterior. Se trata de Mohenjo-Daro, que fue una ciudad de la antigua cultura del Valle del Indo. Sus ruinas se encuentran en territorio del actual Pakistán. El actual nombre Mohenjo Daro significa literalmente ‘montículo de la muerte’. Fue habitada durante el tercer milenio antes de nuestra era (entre el 2600a.C. y el 1800a.C.) a orillas del río Indo.
Estos dados que les mostramos en imágenes tienen una diferencia con los romanos, la suma de las puntuaciones de los dados no es 7 como ocurría en aquellos -incluso los de hoy día siempre suman 7-. Además estaban hechos en arcilla, generalmente.

Las matemáticas y el juego han ido unidos a lo largo de la historia, y en este lugar, en Mohenjo-Daro se dieron ambos. AMJ
