La geometría barroca de Leonardo Sinisgalli(1908-1981), un renacentista en el siglo XX.

 

"Todavía se me escapa una figura de mis compañeros de infancia, una figura que siempre he tratado de atrapar entre las muchas tan dulcemente complacientes que se han enredado en mis páginas. Es Giuseppe, el pequeño monstruo, hijo de Rosa Mangialupini. ¿Quién puede decirlo?" me hubiera dicho que en la forma de los altramuces, convenientemente ampliados, vería un día hacerse realidad el sueño de Gauss, el sueño de una geometría no euclidiana, una geometría barroca como me gusta llamarla, una geometría que aborrece la de anteayer, en una de mis visitas semanales al profesor Fantappiè, profesor de Análisis del Seminario de Matemáticas Avanzadas, conocí un simulacro mucho más complejo que la forma de los altramuces, la superficie romana de Steiner. Es una superficie cerrada de cuarto orden con una variable compleja. Es una forma curiosa, la que he visto, un tubérculo del tamaño de una piedra, con tres ombligos. El matemático alemán Steiner lo encontró en el Pincio mientras meditaba, una mañana de 1912, en el Pincio, sentado justo en uno de esos bancos donde yo, de niño, iba a leer las canciones de Maldoror .. Incluso los geómetras dejaron ese adjetivo delante de la forma, la llamaron romana. TS Eliot, en la canción de Simeon, evoca los jacintos romanos: "Los jacintos romanos florecen en los jarrones..." tradujo Montale. Y quién sabe por qué en mi mente casé las dos imágenes: los jacintos y esta extraña fruta matemática, una fruta de los jardines mediterráneos, una especie "Todavía se me escapa una figura de mis compañeros de infancia, una figura que siempre he tratado de atrapar entre las muchas tan dulcemente complacientes que se han enredado en mis páginas. Es Giuseppe, el pequeño monstruo, hijo de Rosa Mangialupini. ¿Quién puede decirlo?" me hubiera dicho que en la forma de los altramuces, convenientemente ampliados, vería un día hacerse realidad el sueño de Gauss, el sueño de una geometría no euclidiana, una geometría barroca como me gusta llamarla, una geometría que aborrece la de anteayer, en una de mis visitas semanales al profesor Fantappiè, profesor de Análisis del Seminario de Matemáticas Avanzadas, conocí un simulacro mucho más complejo que la forma de los altramuces, la superficie ro de tomate singular, un tomate -por así decirlo- con tres ganchos. Piensa en esos líos que hacen hoy los fruticultores, cuando plantan una semilla dentro de otra o tres semillas, atadas en una, cuando se casan con el lirio o la rosa; piense en la cidra, con gajos internos de limón y naranja, de la rareza de la que Redi escribió al príncipe Leopoldo. Bueno, esta forma hace pensar en hermanos y hermanas siameses. Profesor Conforti, Profesor Severi, Profesor Fantappiè,Lacerta faraglionis , la lagartija azul que vive solo en los farallones de Capri, en el hábitat más pequeño conocido en la tierra. “Esta superficie” dije “es una fruta romana, como la alcachofa”. Pero Severi, Conforti y Fantappiè en cambio enumeraron todas sus maravillosas propiedades: cuatro círculos generadores, tres polos triples, un área calculable por integrales racionales, y luego no sé qué otras diabluras. Me pareció oír a Linneo hablando de alcachofas: carciopholus picassianus , carciopholus guttusii , carciopholus pipernensis aut romanus. (...) Pero la superficie romana de Steiner más que el humus de Testaccio y los jardines Gianicolesi, más que el hierro fértil de los suburbios parecía labrada por el aire y la luz de Roma, como un hermoso guijarro de travertino: era una esponja de piedra caliza con tres agujeros, tres acciaccature, tres cavidades. Una forma con tres jorobas, un Borrominate, eso es todo. Imagina una esfera elástica, presionada por las puntas de tres conos. Debía de tener especiales virtudes acústicas, debía tener un oído muy fino, porque en realidad era todo oídos, parecía una sonda acústica bajada al espacio. Incluso los jorobados tienen pinnas muy receptivas. Están allí continuamente en alerta detrás de las cortinas, detrás de las puertas de los favoritos de los Reyes, estos malditos monstruos no perdieron una sílaba que salió de la boca de las concubinas reales, ni un bostezo, ni un estornudo. Y así mi amigo de la infancia Giuseppe Mangialupini. Fue a informar al Arcipreste de todos nuestros discursos". (...) 

Leonardo Sinisgalli, Carciopholus Romanus . En la locura matemática , Milán, Mondadori, 1950 

  

Leonardo Sinisgalli (1908-1981), poeta, prosista, ensayista además de ingeniero, técnico, publicista, fundador y director de revistas como Pirelli o Civiltà delle Macchine , con estudios matemáticos de primer orden fue uno de los más brillantes intelectuales de el siglo pasado, uno de los pocos en Italia, con Gadda y Calvino, que consideraron la cultura humanística y científica con el mismo interés, asignándoles igual dignidad o no considerándolas separadas. Antes de graduarse en ingeniería industrial en 1931, había asistido a la facultad de matemáticas de Roma, experimentando el fervor intelectual de un ambiente animado por algunos de los más grandes matemáticos italianos, como él mismo recuerda en Carciopholus . 

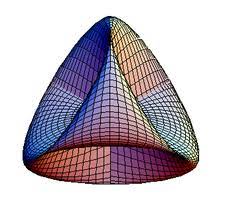
La historia se centra en una superficie algebraica conocida como Roman de Steiner., descubierta por el matemático suizo Jakob Steiner (1796 - 1863) durante una estancia en Roma en 1836 (y no en 1912 como indica erróneamente Sinisgalli). Es un cuartico con infinitos puntos singulares que juntos forman tres rectas dobles que se cortan en un punto, un punto triple para la superficie. El modelo de esta superficie, que se asemeja a un tetraedro con las caras aplanadas en el centro hasta encontrarse, debió estar presente en el Instituto, ya que entonces se utilizaba con fines didácticos. La forma curiosa, y el nombre que lo caracteriza, inspiró a Sinisgalli a combinarlo con el humilde lupino, luego con el tomate (me imagino un "corazón de buey" degenerado), finalmente con un producto típico y célebre de los jardines de Lazio, el Roman alcachofa, la redonda.

En la década de 1930, dos movimientos artísticos diferentes, los surrealistas y los constructivistas, descubrieron el valor estético de los modelos de superficie cúbicos y cuárticos más o menos simultáneamente, sin embargo, la relación entre los modelos de superficie algebraicos y el mundo del arte fue temporal y superficial. Nunca hubo un diálogo entre los matemáticos que construyeron esos modelos y los artistas que los utilizaron como fuente de inspiración. El mundo del arte los consideraba como objetos de los que los constructores no habían sido capaces de captar la calidad estética. Leonardo Sinisgalli, gracias a su competencia matemática, no sólo captó su valor estético, sino que llegó a proponerlos para la inspiración de "arquitectos, ingenieros y diseñadores industriales". Así escribió en el ensayo Geometría barroca, publicado en el Pirelli de junio de 1950, el mismo año que el Furor Mathematicus:

Esos cuerpecitos, algo mayores que un puño cerrado o una piña, habían sido construidos punto por punto según el método cartesiano partiendo de una ecuación de x , y , z , y atribuyendo una doble serie de valores a x e y . Es un método ya familiar para los constructores de aeronaves o motores, un método representativo que transforma una expresión algebraica en una forma (línea o superficie) plana u oblicua, continua o discontinua. La figura resultante de estas operaciones hace visibles todas las singularidades algebraicas de la ecuación. ¿Quién no sabe que una ecuación de primer grado en x e y es la imagen de una recta y que los coeficientes dex e y (su relación de hecho) determinan la inclinación de la línea recta? 

Como decía, por tanto, un geómetra lee en las ecuaciones lo que nosotros leemos en las figuras. Un agrimensor sabe que una diferencia en la escritura se convierte en una caracterización somática de la forma. (…) 

Leonardo Sinisgalli(1908-1981), un renacentista en el siglo XX. AMJ

(Del extraordinario blog Popinga)