El problema de la braquistócrona.
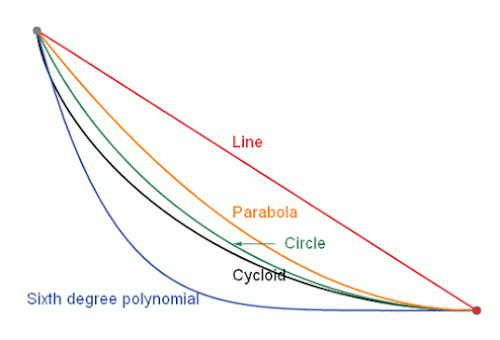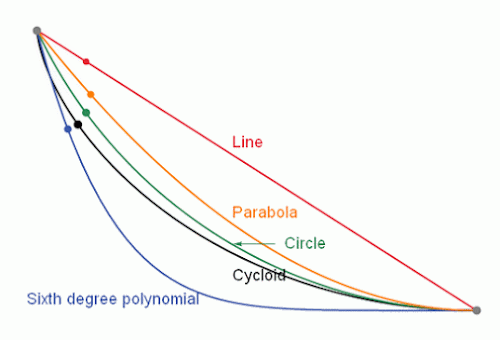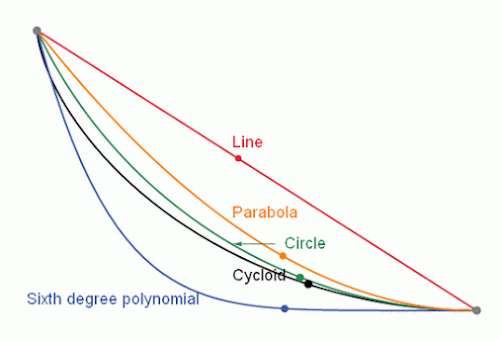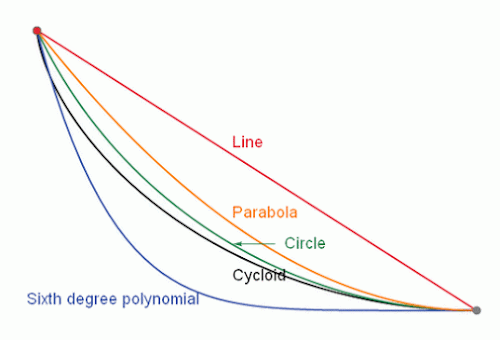
Se trata del siguiente problema: tenemos dos puntos a diferente altura; los conectamos por una rampa y dejamos caer una esfera –pelota- desde el punto más alto. ¿qué tipo de rampa debemos utilizar para que tarde el menor tiempo posible, bajando por su propio peso? Sabemos que el camino más corto es la línea recta, pero ¿será, igualmente, donde tardaremos menos tiempo? Pues no, no se trata de espacio, sino de tiempo. Ésta es la braquistócrona (del griego βραχίστος brachistos ’el más corto’, χρόνος chronos ’tiempo’), la curva del descenso más rápido. La curva que es recorrida en menor tiempo por un cuerpo que comienza en el punto inicial con velocidad cero y sin rozamiento se desliza bajo la acción de la gravedad hasta llegar al segundo punto. En su solución intervinieron los hermanos Jacob y Johann Bernouilli –que al final fueron quienes resolvieron el problema-, L’Hôpital, Leibniz, Newton, entre otros. En esta animación puede verse el resultado, comparando con varias trayectorias posibles:
La braquistócrona es precisamente la cicloide –invertida-, la curva generada por un punto de una circunferencia, cuando ésta gira sobre una recta sin deslizarse. En su estudio intervinieron desde Galileo hasta Fermat, pasando por Pascal, Leibniz o los Bernouilli. Esta curva además de ser braquistócrona, también es tautocrónica -si tenemos una cicloide que cuelga hacia abajo y dejamos caer esferas desde cualquier punto de ella, llegarán abajo a la misma vez-. Varias curiosidades en una misma curva:

La demostración pueden verla en Wikipedia. En este enlace interactivo pueden crear cicloides a su antojo y comprobar las propiedades reseñadas: pcmap.unizar.es
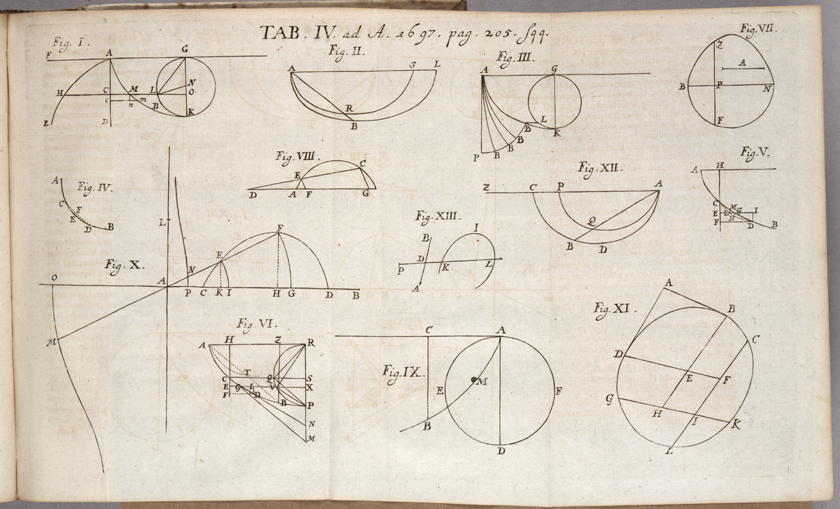
En esta tabla (escrita por Bernouilli en Acta Eruditorim, en 1697)pueden ver las distintas explicaciones gráficas de los que intervinieron en la polémica, a finales del siglo XVII:
La resolución de este problema dio lugar a una nueva rama en el estudio de las Matemáticas: el Cálculo de Variaciones. Sin duda curiosa e interesante. AMJ
1 comentario
Pasquale -