El presidente James Abram Garfield y el teorema de Pitágoras.

Un día como hoy, 19 de Septiembre de 1881 murió asesinado el 20º presidente de los Estados Unidos, cuando llevaba 6 meses y 15 días en el cargo. ¿Pero qué hace aquí un presidente de los EEUU? Pues nada más y nada menos porque, entre otras, tenía una afición especial: las matemáticas. De formación muy completa, llegó a enseñar idiomas clásicos y se licenció en derecho por su cuenta.Viendo que su futuro no era el docente se dedicó a otros menesteres.Así se incorporó a la política siendo senador por Ohio, por el Partido Republicano y fue investido Presidente en 1881.En Junio de ese mismo año fue herido en un atentado, sobreviviendo 70 días, hasta que murió el 19 de Septiembre, aunque dice que no por los disparos sino por lo mal que fue curado por su equipo médico. Pueden verse biografías en los enlaces siguientes: http://www.cokmo.com/james-abram-garfield , o en http://es.wikipedia.org/wiki/James_A._Garfield , o también en http://americanhistory.about.com/od/jamesgarfield/p/pgarfield.htm o en la página web de la propia Casa Blanca http://www.whitehouse.gov/about/presidents/jamesgarfield .

Aunque aparece en todas sus biografías como una anécdota su afición por las Matemáticas, publicó en el New England Journal of Education una original demostración del Teorema de Pitágoras. Es la siguiente extractada de la Wikipedia:

Garfield construye un trapecio de bases a y b, y altura (a+b), a partir del triángulo rectángulo de lados a, b y c. Dicho trapecio resulta compuesto por tres triángulos rectángulos: dos iguales al dado, y un tercero, isósceles de catetos c. En consecuencia:

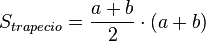$S_{trapecio}=frac {a+b}{2} cdot (a+b)$ como corresponde a la superficie del trapecio, pero asimismo tenemos una figura compuesta por tres triángulos, dos de ellos iguales, de modo que:

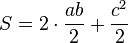
$S=2 cdot frac {ab}{2} + frac {c^2}{2}$

igualando las ecuaciones anteriores obtenemos:

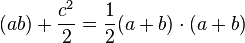
$(ab) + frac {c^2}{2} = frac {1}{2} (a+b) cdot (a+b)$

pasando el $1 / 2$ al otro miembro y simplificando ...

$2 a b + c 2 = (a + b) 2$

expandiendo el miembro derecho ...

$2 a b + c 2 = a 2 + 2 a b + b 2$

restando $2 a b$ a ambos miembros, finalmente nos da:

^{C 2}=a²+ b²y el teorema está demostrado.

Entre la clasificación de las demostraciones del Teorema de Pitágoras (en total 78) recogidas por http://www.cut-the-knot.org/pythagoras/index.shtml#5 ,la de Garfield aparece la quinta, en elegancia y originalidad.

(En un sello de la República de Liberia.)

Como acabamos de ver la Presidencia de Estados Unidos no está reñida con la inteligencia, aunque últimamente lo parecía, dados los discursos dirigidos a la nación y a sus ciudadanos que todos hemos oído y que pueden verse en las hemerotecas. AMJ

19/09/2011 17:40 A.M.J. Enlace permanente. Informes y documentación matemática.

Comentarios » Ir a formulario

Autor: jose Seleme