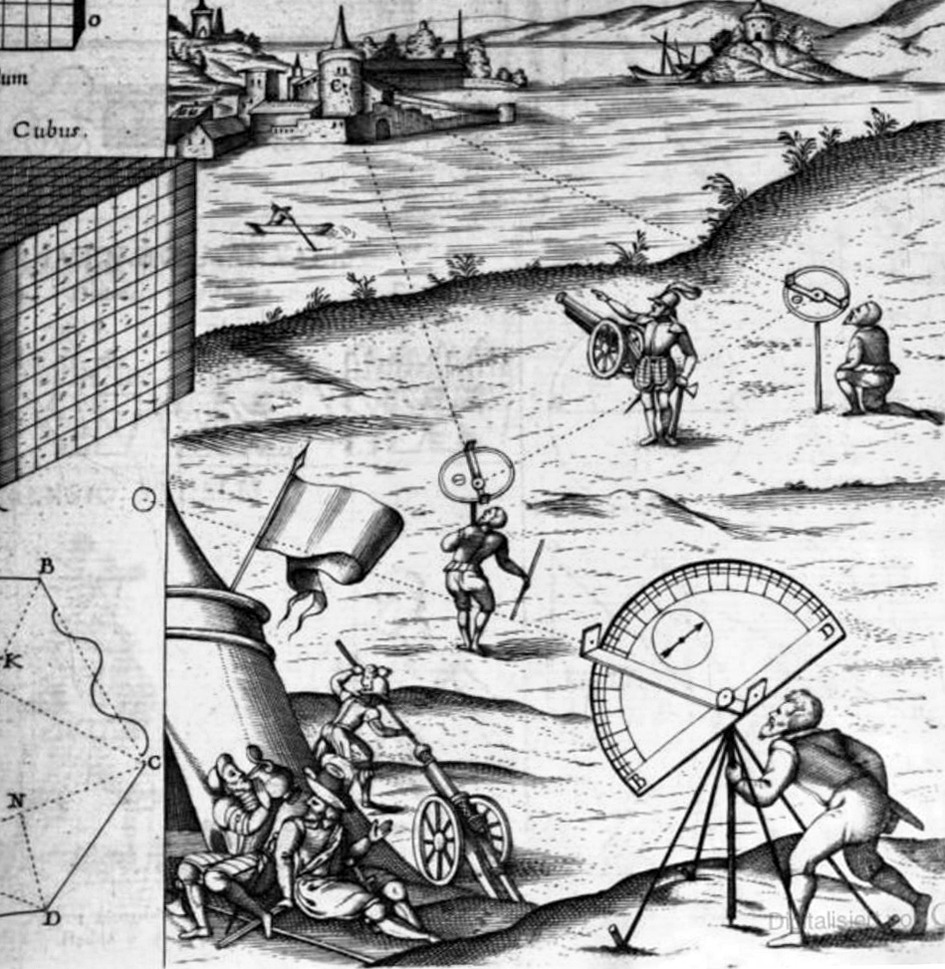
Juan Caramuel Lobkowitz (1606, 1682) fue un matemático, filósofo, lingüista y monje cisterciense español. Nacido en Madrid, ya a los doce años mostraba su talento para crear tablas astronómicas –oficio al que se dedicaba su padre. Después de estudiar Filosofía y Humanidades en Alcalá y Teología en Salamanca, su predilección por las lenguas le hizo dominar casi 20 idiomas. Llegó a ser abad en Praga y obispo en Italia. Aprendió de los eruditos más célebres de la época: Descartes, A. Kircher, el astrónomo von Rheita y el astrónomo belga G. Wandelen.

Su curiosidad infinita por todo tipo de cuestiones le llevó a planteamientos generalistas, sin tratar un problema como tal, sino teniendo en cuenta todas las perspectivas posibles. Por ese acumulo de talento y sapiencia llegó a llamársele el Leibniz español. Llegó a escribir sobre todo: poesía, teatro, filosofía, música, política, teología, matemáticas, astronomía, física,… y un largo etcétera; y se le cuentan más de 260 obras, aunque sólo 60 impresas.
En Matemáticas, que es lo que nos concierne, estudió Teoría de la Probabilidad: al parecer Pascal se inspiró en su obra -«Kybeia, quæ combinatoriæ genus est, de alea et ludis Fortunæ serio disputans -enlazada completa en latín-» (1670),- para profundizar en su formulación probabilística. Ese libro de probabilidad fue el segundo tratado de Probabilidad después del de Huygens, donde el español estudia problemas de juegos y apuestas. Este libro –de 22 páginas- está incluido en otro volumen mayor –Mathesis bíceps, 1670-, que también incluye la primera descripción impresa del sistema binario, con un adelanto de unos 30 años a Leibniz, quien la divulgó. (Vean en este enlace de books,google un avance muy generoso de este libro Mathesis bíceps). Esta obra, con sus 1800 páginas, constituye una enciclopedia de las matemáticas hasta esa fecha y en el que sus aportaciones en Probabilidad ocupan las páginas desde 972 hasta 995(Ver revista Suma).
 | 
|
![speciesbarocus: Juan Caramuel y Lobkowitz - Mathesis biceps (1670). Detail. [x]](http://41.media.tumblr.com/7ed03e607e63482460fc5e33ae95f435/tumblr_myesgz6Qj01qe866ho1_1280.jpg) | ![speciesbarocus: Juan Caramuel y Lobkowitz - Solis et artis adulteria (1644). [x]](http://40.media.tumblr.com/082fe58fc4bcd5a9b9b4586a607ceee0/tumblr_mygof78pV51qe866ho1_1280.jpg)
|
También fue el primer español que publicó una tabla de logaritmos y desarrolló un sistema de logaritmos en base 109. Además, en Astronomía, creó un método para determinar longitudes utilizando la posición de la Luna; y en Trigonometría propuso un nuevo método para trisecar un ángulo. En Arquitectura, además de escribir mucho sobre esta materia, diseñó la fachada de la catedral de Vigevano, de donde fue obispo. Su tratado de aruitectura fue uno de los textos más innovadores en la arquitectura publicadas en su momento, el estudio de la curva, o las aplicaciones de los órdenes clásicos en circunstancias irregulares, tales como superficies convexas y cóncavas, escaleras, circular y espacios ovalados.

(Catedral de Vigevano, Italia)
Un español completo, como pocos, un auténtico hombre universal barroco -como dice de él, Juan Velarde- pero que ha pasado desapercibido en la Historia de España y en la Historia de la Ciencia, donde debía haber ocupado el sitio que merecía. Ya lo hemos dicho en multitud de ocasiones. En este país, ni ahora ni antes ni nunca, se le reconocen los méritos a nuestros paisanos ¡Y así nos va! El país de la envidia y el rencor. Pero,¡¡ qué vamos a hacer, es el nuestro y el único que tenemos!! AMJ
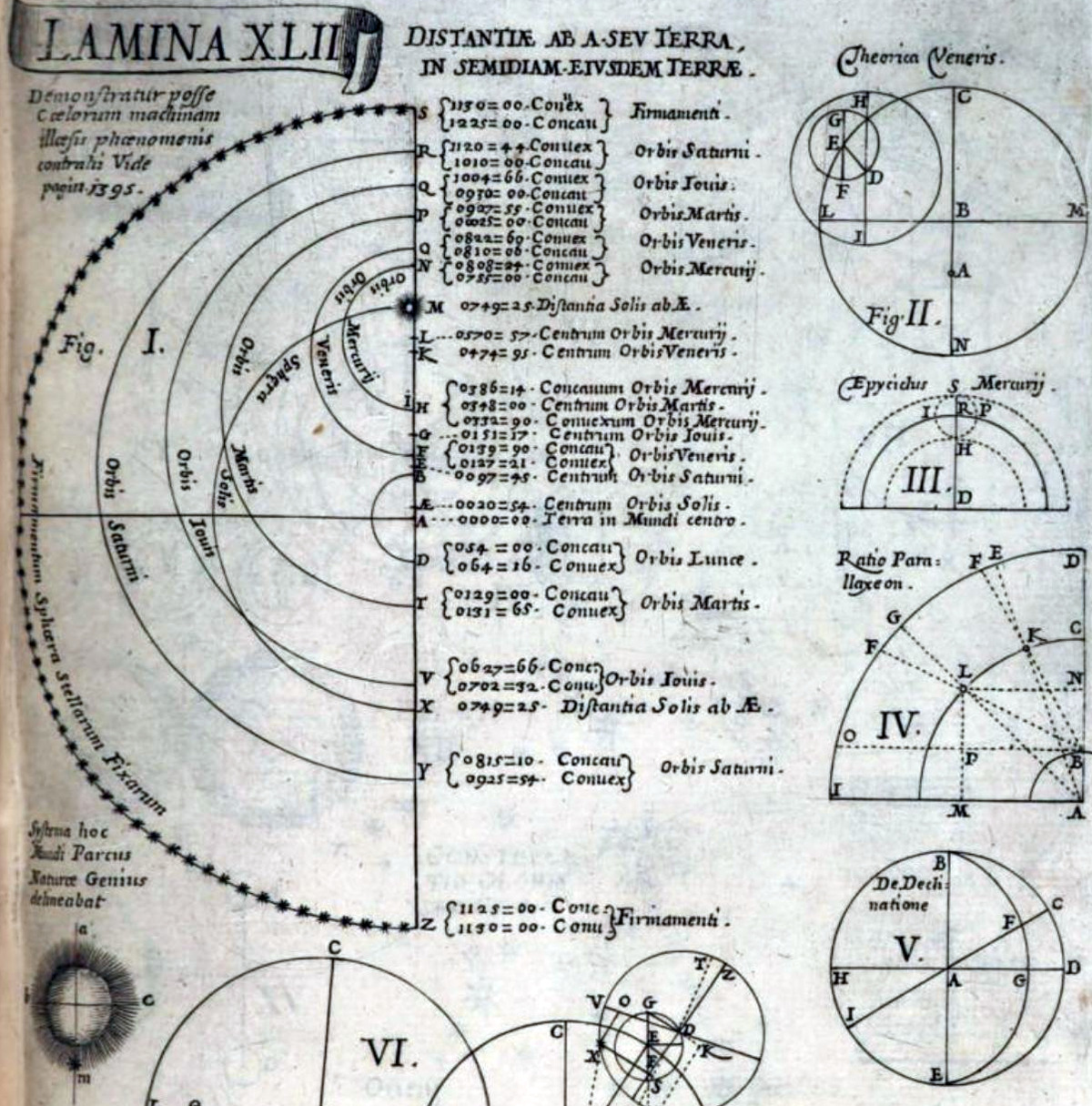





















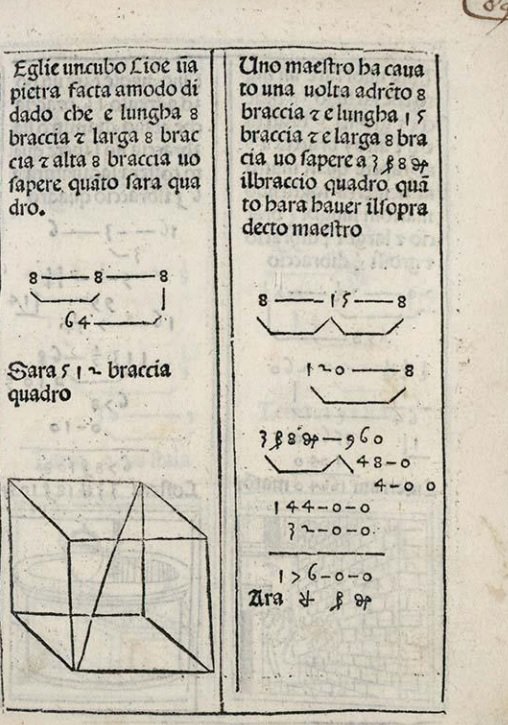
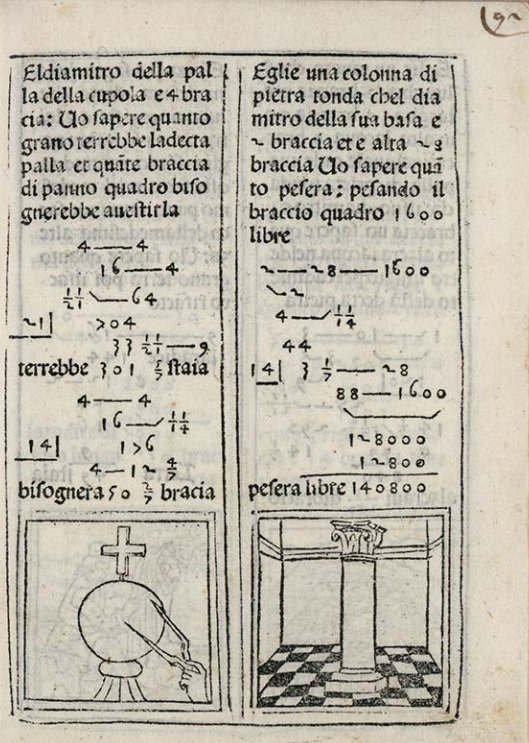

















































![speciesbarocus: Juan Caramuel y Lobkowitz - Mathesis biceps (1670). Detail. [x]](http://41.media.tumblr.com/7ed03e607e63482460fc5e33ae95f435/tumblr_myesgz6Qj01qe866ho1_1280.jpg)
![speciesbarocus: Juan Caramuel y Lobkowitz - Solis et artis adulteria (1644). [x]](http://40.media.tumblr.com/082fe58fc4bcd5a9b9b4586a607ceee0/tumblr_mygof78pV51qe866ho1_1280.jpg)