El beso preciso de Frederick Soddy.
El Premio Nobel de Química de 1921 por el descubrimiento de los isótopos, Frederick Soddy, se dedicó también a las Matemáticas y a la poesía. Ésta última es la poderosa razón por la cuál lo traemos por aquí. El poema El beso preciso(The Kiss precise), publicado en Nature en 1936, acompaña a un teorema de Geometría, conocido como Teorema de Soddy, que dice que si tres círculos son tangentes exteriores dos a dos, entonces existen otros dos círculos tangentes a esos tres, uno exterior y otro interiormente. El poema lo cuenta así:
Pueden besarse los labios, dos a dos,
sin mucho calcular, sin trigonometría;
mas ¡ay! no sucede igual en Geometría,
pues si cuatro círculos tangentes quieren ser
y besar cada uno a los otros tres,
para lograrlo habrán de estar los cuatro
o tres dentro de uno, o alguno
por otros tres a coro rodeado.
De estar uno entre tres, el caso es evidente
pues son todos besados desde afuera.
Y el caso tres en uno no es quimera,
al ser éste uno por tres veces besado internamente.
Cuatro círculos llegaron a besarse,
cuanto menores tanto más curvados,
y es su curvatura tan sólo la inversa
de la distancia desde el centro.
Aunque este enigma a Euclides asombrara,
ninguna regla empírica es necesaria:
al ser las rectas de nula curvatura
y ser las curvas cóncavas tomadas negativas,
la suma de cuadrados de las cuatro curvaturas
es igual a un medio del cuadrado de su suma.
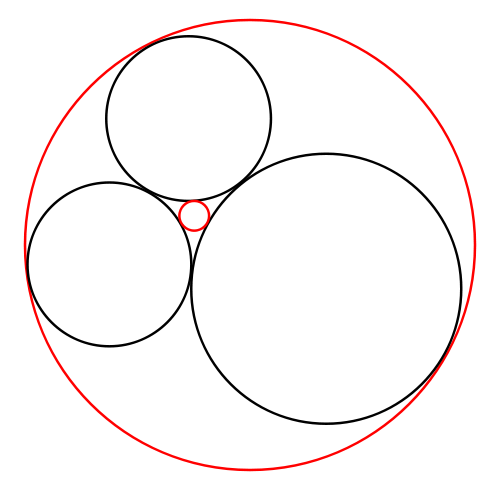
Esta primera parte es lo que se conoce como Teorema del Círculo de Descartes, que lo mencionó en una carta a la princesa Isabel I de Bohemia, aunque ya había sido estudiado por Apolonio en el siglo III a.C. Soddy lo generaliza para cinco esferas, y termina así el poema:
Espiar de las esferas
los enredos amorosos
pudiérale al inquisidor
requerir cálculos tediosos,
pues siendo las esferas más corridas,
a más de un par de pares
una quinta entra en la movida.
Empero, siendo signos y ceros como antes
para besar cada una a las otras cuatro,
El cuadrado de la suma de las cinco curvaturas
ha de ser triple de la suma de sus cuadrados

Incluso Gosset, un matemático aficionado, también en 1937, añade estrofas al poema, con una generalización a espacios n-dimensionales:
No debemos empero confinar nuestros cuidados
a los simples círculos, esferas y planos,
sino elevarnos a n-espacios e hipercurvaturas
donde también las múltiples tangencias son seguras.
En n-espacios, los pares de tangentes
son hiperesferas, y es verdad,
–mas no evidente–,
cuando n + 2 de tales se osculean
cada una con n + 1 compañeras
que el cuadrado de la suma de todas las curvaturas
es n veces la suma de sus cuadrados.
Ver más en Ztfnews.wordpress.com , www.pballew.net o en www.ams.org
Este maravilloso poema viene a demostrar que le ciencia no está reñida con el resto de las artes, solamente está separada por los que nos hicieron estos catastróficos planes de estudios que encerraron a cada especialidad en su corralito, trasladando la impresión a los alumnos que son campos separados. La interconexión existe y desde este blog tratamos de probarlo, en nuestro afán de acercar la matemática al arte, la literatura, la sociedad, la economía,… y viceversa. AMJ

0 comentarios