La esponja de Menger.

La esponja de Menger es un fractal descrito en 1926 por Kart Menger, cuando trataba el concepto de dimensión topológica. Es un conjunto compacto, no numerable y de medida de Lebesgue nula. Su dimensión fractal de Hausdorff es log20/log3= 2,7268….pero de dimensión topológica 1. Tiene una superficie infinita, pero volumen 0. Su construcción es: 1º Comenzamos por un cubo; 2º Dividimos cada cara del cubo en 9 cuadrados, formando así 27 cubos; 3º Quitamos los cubos centrales de cada cara y el cubo central, quedando 20 cubos, 4º repetimos con los 20 restantes la mismas 3 operaciones anteriores. Tras un nº infinito de iteraciones, lo que nos queda es la esponja de Menger. Vean una animación, casi escandalosa: no para. El paseo casi se convierte en agobiante. AMJ
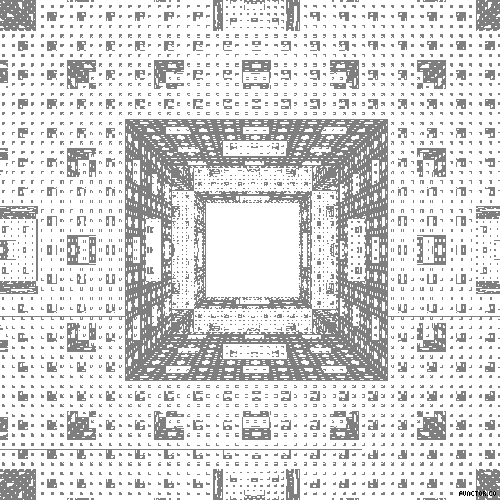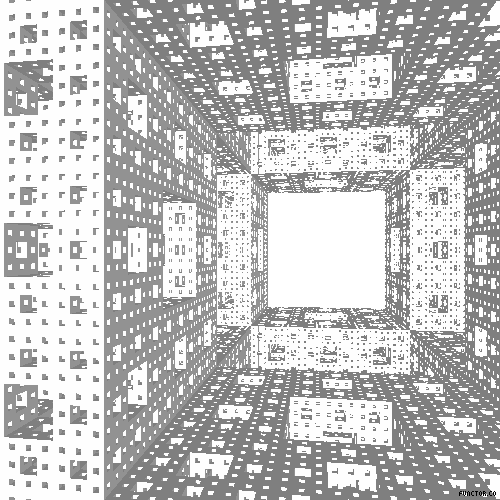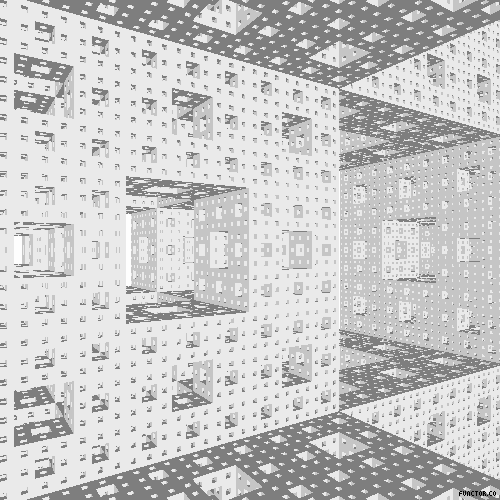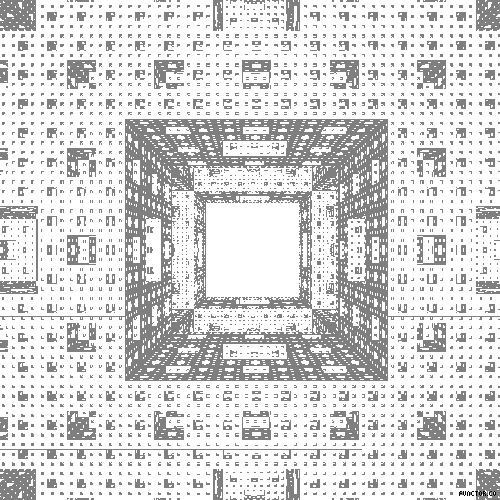
0 comentarios