Mujeres y Matemáticas

Clelia Grillo Borromeo y la curva de la rosa.

Nacida en Génova en 1684 dentro de una familia de la nobleza italiana, dominaba ocho lenguas y fue autodidacta en Ciencias, Mecánica y Matemáticas –disciplina para las que tenía una especial habilidad-. Se casó con Bartolomé Borromeo, pero a su suegro –que llegó a ser virrey de Nápoles- no le gustaba que la mujer de su hijo frecuentara ambientes científicos y catalogada en esos ambientes como excéntrica. Eso le trajo bastantes problemas, ya que en palacio sólo recibía a científicos, naturalistas  y matemáticos. Pero también le gustaba el juego. Sí, el de las apuestas: perdió. Su proyecto de crear “La Academia de los Vigilantes” fracasó, pero mientras estuvo   funcionando, fue el centro de la vida académica y científica de Milán.

Tuvo ocho hijos, pero eso no le impidió seguir adelante con su vida académica y tertuliana, carteándose con los más afamados matemáticos de la época. Entre ellos Guido Grandi, difusor de los avances de Leibniz en Italia. Uno de sus libros más importantes fue Flores Geometrici, un compendio de los diferentes tipos de curvas estudiados en las flores. En concreto, estudiaba los pétalos de las rosas. Clelia Grillo  descubrió una curva especial – sobre superficies esféricas- y en su libro- que le dedicó a Clelia-, Grandi, la llamó Clelie, en honor a su descubridora.

En 1746 cuando estalla el conflicto entre España y Austria, muerto ya su marido, toma partido por España –una vez más en el bando equivocado-, y estando Milán bajo ocupación austriaca, tuvo que abandonar la ciudad y sus bienes fueron confiscados. Al acabar el conflicto vuelve a Milán, como una heroína. Le hacen honores y homenajean por todos los rincones. Hasta 1877 –cuando muere- abandona ya un poco sus labores alrededor de la Ciencia y se dedica más a otras actividades, como el teatro, la poesía y la historia.

Sin lugar a dudas, Clelia fue una mujer especial, que no pasó desapercibida a los ojos de Montesquieu, en sus viajes a Italia, quien dijo de ella “la mujer más admirable del Universo”, asombrado por su vitalidad intelectual, su curiosidad inagotable, su personalidad indomable y, en consecuencia, singular. Sin duda, adelantada a su tiempo. AMJ

Philippa Garrett Fawcett, en la cima de la matemática victoriana.

 Hoy, 8 de Marzo, se celebra el día de la mujer trabajadora. Ya en años anteriores hemos hecho mención a ello, desde nuestra óptica de mujeres que han sobresalido en la ciencia matemática y las dificultades que han  tenido que superar. Ver 8 Marzo 2013, día de la mujer trabajadora..

Traemos hoy por aquí a una matemática desconocida, Philippa Garrett Fawcett (4 Abril 1868 - 10 Junio 1948) . Y ella va a ser la muestra de las mujeres luchadoras, inteligentes,… pero que su condición le hizo renunciar a un porvenir que, por la época que le tocó vivir, estaba vedado para el género femenino. Contemos un poco su historia.

 Philippa era hija de Henry Fawcett -ciego desde los 25 años de edad-, un catedrático de Economía Política en Cambridge y Director General de Correos en el Gobierno de Gladstone. Su madre era Millicent Garrett Fawcett, líder del movimiento por el sufragio universal y hermana de Elisabeth, la primera mujer médica británica. Por lo que empezamos a ver se trataba de una familia de clase alta, instruida,  luchadora y tenaz: no se iba a arredrar por contratiempo alguno.  Con quince años mostraba una habilidad excepcional para las Matemáticas y sus padres contrataron a un tutor para que le ayudase.  Ya que no podía estudiar matemáticas en Cambridge al mismo nivel que los hombres, su padre le dispuso clases de Matemáticas en la University College London, donde se permitía el estudio a mujeres, pero de un nivel más bajo de lo que ella pretendía.   Más tarde  pudo entrar en el Newnham College -colegio femenino  adscrito a la Universidad de Cambridge-  donde sobresalía en Álgebra y Geometría, lo que le auguraba éxitos futuros.

(Con su equipo de hockey)

 Eran pocas las mujeres que en el siglo XIX –aunque ya a finales- se atrevían a estudiar en la Universidad: estaba mal visto no dedicarse a las labores para la que “estaban predestinadas”. Fundamentales eran la maternidad y el hogar. Así pasó a lo largo de la Historia. La Universidad de Cambridge era, probablemente, la de mayor prestigio del mundo; y los alumnos que terminaban la carrera de Matemáticas realizaban una serie de pruebas para lograr, el que obtuviese máxima puntuación, el “Senior Wrangler”, distinción que data de 1748 y que aún hoy se realiza –entre otros ganadores están Arthur Cayley, Stokes y Frank Ramsey-.   Esta distinción tan prestigiosa le suponía al ganador una carrera  académica brillante y como muestra: más de nueve premiados ocuparon la cátedra Lucasiana de Matemáticas de U. de Cambridge, que entre otros también fue ocupada por Newton y ahora por Stephen Hawking.  Eran tan duras las pruebas, que como anécdota contaremos que el ganador de 1855, James Savage, fue encontrado muerto de apoplejía(¡hoy, ictus cerebral) tres meses más tarde, debido a los esfuerzos desmesurados que hubo de hacer para la prueba(sic).

(A la edad de 15 años)

Cámara del Senado de Cambridge, donde se leían los resultados del Senior Wrangler.

Las pruebas duraban 8 días y se debía contestar a las 192 preguntas que aparecían en 12 cuestionarios, cada vez de mayor dificultad. Una prueba de 63 preguntas más durante 3 días era el final de la prueba, para los que habían obtenido las máximas puntuaciones en la primera fase. Pues bien, estamos en 1890. La Universidad de Cambridge permitía presentarse a las pruebas a las mujeres, pero no les permitía que ganaran (¡¡esa moral victoriana!!). El 7 de Junio, de ese año 1890, dieron a conocer los resultados de la edición anual.  Al llegar a las puntuaciones de las mujeres, el encargado de dar la noticia, dijo: “Miss Philippa Garrett Fawcett, por encima del Señor Wrangler”. Fue a lo máximo que se atrevió. No estaban los tiempos para desmontarlo todo tan rápido.  Había obtenido una nota un 13% más alta que su inmediato seguidor, un varón, G.T. Bennett, que fue proclamado Señor Wrangler del año 1890 y se llevó todos los parabienes de tan alta distinción.

La madre de Philippa, Millicent, militante feminista y sufraguista.

Newnham College, de la U. de Cambridge.

La fiesta no se hizo esperar: repicaron las campanas, hogueras en los campos de de hockey,… y por supuesto, fue llevada a hombros (¡¡como los toreros en España: a hombros por la Puerta Grande!!). La acogida masculina de la noticia fue aceptable, pero, de todas maneras, en 1921 una votación impedía que las mujeres fueran aceptadas en la Universidad de Cambridge en las mismas condiciones que los hombres – de hecho fueron destrozadas las puertas de la sala donde se procedía a la votación, en protesta por la decisión-.

Esta noticia corrió como la pólvora por todo el mundo: The New York Times le dedicó una columna y propició  la apertura de los estamentos académicos hacia las mujeres. Pero todavía tuvieron las mujeres que esperar bastante para acceder a las Universidades en las mismas condiciones que los hombres para graduarse: Gottingen en 1919, Oxford en 1920, Yale en 1969 y Harvard en 1977. En Cambridge en 1948, las mujeres pudieron graduarse junto a los hombres.

(Diario de Philippa, de un viaje a la India entre 1899-1900)

Estos acontecimientos desmontaron las creencias de la mujer como sexo débil, como inferior, matemáticamente hablando, que ya en otras especialidades se habían superado. El último bastión de “machismo científico victoriano” fue derrumbado por esta joven de 22 años – primera mujer por encima del Senior Wrangler y la última, porque desde 1909 cambió el sistema dada la especificación de las matemáticas-. Desmontó las teorías del desarrollo humano del final del siglo XIX, según las cuales el cuerpo sólo tenía energía disponible para el desarrollo físico o intelectual, al entender que era un sistema cerrado(¡de energía invariable!) y al entender que el sistema reproductivo de la mujer era más complicado que el de los hombres, los recursos energéticos que había que dedicar desde el organismo eran mayores, por lo que su plano intelectual era, simplemente, inferior(¡¡¡”cerebro y ovario no podían desarrollarse al mismo tiempo” , o “la medición del volumen craneal femenino constataban su inferioridad” defendían!!!). Estas teorías eran defendidas por sesudos científicos, pero que, este caso y otros parecidos, las campañas de los defensores de las causas femeninas –entre otras, las luchadoras por el sufragio femenino-, terminaron por ser abandonadas  por sus seguidores.

 Fue más tarde galardonada con una beca para seguir estudiado en el Newnham College, el colegio para mujeres de la Universidad de Cambridge, fundado en 1871; convirtiéndose  en profesora del colegio durante diez años. Sus estudios de investigación en ese tiempo fueron la dinámica de fluidos y en 1902 deja Cambridge para ayudar en Sudáfrica al desarrollo de la educación. De vuelta a Inglaterra ocupó un puesto en el London County Council, desarrollando la educación secundaria, retirándose en 1934 después de haber ocupado el más alto puesto por una mujer en ese organismo. 

(Nominación de un Senior Wrangler en 1842)

Philippa Fawcett  lo consiguió. Llegó a ver  a sus 80 años que Cambridge, en 1948, se había abierto a las mujeres, y después, un mes después, en Junio murió. Plácidamente. Había vencido a la sinrazón humana: los cerebros masculinos no son superiores a los femeninos. Y ya está. No hay más. Nada más. Sólo reconocerle desde este humilde blog  su entrega, su lucha, su talento, y que hoy 8 de Marzo  reivindicamos.

Enlaces para profundizar en su biografía en Naukas, smithsonianmag.com, agnescott.edu, history.mcs.st-andrews.ac.uk y yorokobu.es . AMJ

Olga Alexandrovna Ladyzhenskaya: matemática rusa desconocida, ¿la más grande de la historia?.

Sabemos que por diversas razones, hay pocas mujeres que se han dedicado a la ciencia a lo largo de la historia. Particularmente en Matemáticas han sido pocas las que lo han hecho. Cuando así ha ocurrido hay detrás, de casi todas ellas, una tragedia. Hoy traemos aquí a una desconocida, por lo menos para mí, que cumple fielmente con las adversidades sufridas por el género femenino en su dedicación a la investigación, la ciencia y en nuestro caso, las matemáticas. Se trata de Olga Alexandrovna Ladyzhenskaya, que acompaña a una dilatada vida repleta de sufrimiento una constancia e investigación matemática digna de ocupar un sitio en la historia de esta ciencia.

Nacida en el año 1922 en Kologriv(Rusia), una mente tan brillante tuvo la mala suerte de cruzarse en su camino a Stalin. No es necesario recordar las atrocidades cometidas en el régimen ruso bajo el dictador: asesinatos, expropiaciones, deportaciones masivas, etc, todas ellas de millones de personas. Unos por oponerse al poder establecido, otros por pertenecer a una etnia o grupo que no “le caía simpático”. Ella era hija de un profesor de Matemáticas que descendía de la nobleza rusa y nieta de un famoso pintor ruso, Gennady Ladyzhensky. Si ya la vida era complicada para cualquier ruso de a pie, para ellos fue incluso peor. Tuvieron problemas de alimentos, ropa,…y además un seguimiento especial de la policía, por su procedencia. Tarde o temprano iban a hacerles pagar por ello. Fue en 1937 cuando su padre fue detenido por el NKVD ( la policía secreta rusa, de asuntos internos y precursor del famoso KGB) y ejecutado sin juicio alguno. Previamente había sido señalado como enemigo del pueblo, lo que supuso que sus dos hermanas no pudiesen estudiar, sin embargo a ella si se le permitió, no sin problemas y , seguro, siendo señalada por los demás. Su padre o había previsto con anterioridad: había dado clases a sus hijas desde muy pronto y fue quien inoculó en Olga el “virus matemático”.

La mayoría de su familia había desaparecido en 1940 y los que quedaban y ella tienen que dedicarse a labores artesanales: confección de vestidos, zapatos,…como únicos medios de subsistencia. Después de la escuela secundaria trabajó en la Escuela de Formación de Maestros (durante la II Guerra Mundial disminuyó la persecución de los oponentes por el régimen ruso), aunque se le prohibió matricularse en la Universidad de Leningrado, llegando a dar clases de Matemáticas en el mismo colegio que su padre en Kologriv. En 1943 logra, a través de conocidos, matricularse en la Universidad de Moscú, a la que se traslada con una beca Stalin (¡que sarcasmo!) y una cartilla de racionamiento, para poder subsistir. ¿Qué es lo que estudia? Pues sin duda: Matemáticas. Primero álgebra y teoría de números y ecuaciones en derivadas parciales después, para especializarse en estas últimas. Alumna de Petrosvky, primero, y colega después fue una de sus máximas influencias. Graduada ya se traslada a Leningrado en 1947 donde su amistad con Smirnov y su boda con Kiselev, un especialista en teoría de números, hicieron de nuestra flamante matemática toda una experta. Su matrimonio duró muy poco: ella no quería tener hijos y compartirlos con su obsesión. Todo su tiempo quería dedicarlo a las matemáticas. Eligió su camino. Y nosotros se lo agradecemos. Muchas otras mujeres a lo largo de la historia tuvieron que elegir el camino para el que estaban predeterminadas y la sociedad les había asignado. Menos mal que algunas tomaron el que les dictaba su conciencia.

Se doctoró en 1949, con una tesis del campo de las ecuaciones en derivadas parciales, pero no pudo completarse y publicarse hasta después de la muerte de Stalin, en 1953, lo que supuso de alguna forma su rehabilitación( aunque hasta el discurso de Kruschov en 1956 la apertura no llegó a la URSS). Su primer libro lo publicó, también, en 1953, sobre ecuaciones hiperbólicas y ya en 1954 es nombrada profesora de la Universidad de Leningrado e investigadora de la Steklov –Instituto de Matemáticas-. Así otro libro suyo en la rama de la física matemática “La teoría matemática de flujo viscoso incomprensible” fue un éxito y hoy día es considerado como un clásico de la materia.

Con la llegada en 1989 de la Perestroika, la apertura de Gorbachov, la democracia y la apertura económica se abrieron paso en Rusia, pero un tiempo de penurias económicas de los investigadores y científicos se apoderó de ellos. Pero después de todo lo que había sufrido y resistido no le importó continuar viviendo donde lo hizo toda su vida, adaptándose a los nuevos tiempos. Quedó sorprendida al observar que los avances que había conseguido eran parecidos a los de Leray, pero que al no haber trasvase de conocimientos entre Este y Oeste durante la Guerra Fría esa falta de comunicación hizo que todo avance fuese mucho más lento.

Es considerada como una de las matemáticas más influyentes del siglo XX, y fue premiada en muchas ocasiones: Premio Chebyshev, el Premio estatal de la URSS, Premio Kovalevsky en 1992, la Medalla de Oro Lomonosov entre otros. Acumuló distintos puestos directivos de institutos científicos como: Jefe de laboratorio de Física Matemática de la Steklov, presidenta de la Sociedad matemática de San Petersburgo (antigua Leningrado), etc. Amiga de Alexander Solszhenitsyn (¡que también era matemático, además de premio Nobel de Literatura!) fue considerada toda su vida como un espíritu libre, próximo a la disidencia. Fue también una apasionada del arte y religiosa, de creencias profundas. Solidaria con los desfavorecidos, incluso desatendiendo su propia seguridad. Estuvo trabajando hasta sus últimos días, muriendo en San Petersburgo cerca de cumplir los 82 años, en 2004.

Ver biografías en Wikipedia, rsme o history-mcs. Necrológica en El Pais.

Aunque tuvo problemas de visión durante los últimos años de su vida, ello no le impidió viajar a Occidente a numerosos congresos y recogidas de premios y galardones, - hasta 1989 solo se le permitió salir una vez, en 1958-, y sobre todo tuvo tiempo de resarcirse de las calamidades pasada, por lo menos de vivir libremente, en un país que le reconoció su talento y le admiró hasta su desaparición. Como hemos visto esta desconocida matemática rusa, eclipsada por un régimen totalitario que impidió el desarrollo libre de la Ciencia, el Arte y la Cultura, pero que no pudieron impedir su contribución al avance de la Ciencia, ocupa por meritos propios un lugar en la Historia de las Matemáticas. Sin lugar a duda. Incluso algunos se preguntan si es la más grande matemática de todos los tiempos. desde luego un importante legado nos dejó. AMJ.

María Gaetana Agnesi y la bruja matemática.

No. No es lo que algunos profanos podrían pensar. No se trata de ninguna bruja sino de una curva. Pero ¡que pases a la Historia por una curva que no descubriste y por un nombre: la bruja, procedente de una mala traducción tiene guasa! Pero sobre todo porque se pasa por alto toda la labor de una divulgadora prodigiosa y por obviar su pertenencia, con mayúsculas, a la historia de lucha de la mujer por equiparar sus derechos a los de los hombres.

¿Quién era entonces María Gaetana Agnesi? Nacida en Milán en Mayo de 1718 fue la mayor de ¡¡21 hermanos!! Su padre Pietro Agnesi, que tuvo tres esposas, acaudalado e ilustrado hombre de negocios propició el desarrollo intelectual de María, la niña prodigio, proporcionándole profesores particulares y tertulias científicas que hicieron de ella una de las más preciadas cabezas pensantes de la Italia del XVIII. La precocidad de la infanta es indiscutible, a pesar de la ampulosidad de sus biógrafos (algunos la convierten en políglota ya con 5 años), pero, sin lugar a duda, antes de los trece años dominaba latín, griego, español, francés, hebreo y alemán. Algunas veces las intenciones de los padres de exhibir las capacidades de sus retoños han abundado a lo largo de la historia y en nuestro caso llegaron a convertirse casi en “funciones circenses”: lo mismo explicaba las funciones del cuerpo humano o las diferencias de las teorías heliocéntricas y geocéntricas, que igualmente daba explicaciones científicas sobre las mareas o recitaba un poema, en latín, de un autor romano.

En toda su formación la ciencia y la religión anduvieron unidas. Sus preceptores y educadores fueron siempre religiosos; formaban así un catolicismo ilustrado. El jesuita y geómetra Saccheri, el monje matemático Rampinelli y el jesuita matemático Ricatti formaron un tridente católico y matemático que llevaron a nuestra María, ya casi adulta, a conjugar una unión de Matemáticas y religión que no dejó el resto de su vida. Su intención, consecuentemente, de entrar en un convento no fue el desenlace alocado de una mujer solitaria, retraída e introvertida sino el resultado de una vida dominada, casi, por los hábitos y la contemplación, que únicamente la muerte de su madre-en el parto de su 8º hijo- comprometió a nuestra prócer al cuidado de su padre y de sus hermanos, los existentes y los venideros -vendrían 13 mas-. A cambio obtuvo el compromiso de su padre de no forzarla a más exhibiciones, bailes de sociedad,… y permitirle llevar una vida de estudio y recogimiento en su propia casa.

Ahí tenemos entonces a una María Agnesi “ama de casa”, dedicada al cuidado de sus hermanos e invadida por la tristeza y la aflicción de perder a la mayoría de ellos- la mortalidad infantil en esa época era elevadísima -. Pero en una casa acaudalada su presencia y dedicación al cuidado de la casa y de la familia no era absoluta: tenía tiempo para estudiar, publicar, avanzar,… en todo tipo de estudios en los que se embarcó. Cuando tiene ya 32 años, en 1750, enferma su padre y el papa Benedicto XIV, amante de las matemáticas (¡qué raro, pero hubo algunos con esta inclinación científica , por ejemplo Gerbert D’Aurillac , matemático, que fue el Papa Silvestre II) y conocedor de las obras de María, le ofrece la Cátedra de Matemáticas de la Universidad de Bolonia, por su mérito y valía matemática. Parece que nunca la ocupó y muerto su padre el compromiso adquirido con él llega a su conclusión: la Teología y las obras de caridad ocupan su vida terminando en la miseria. Muere en 1799 en el Hospicio Trivulzio de Milán, institución de beneficencia, que dirigía. Reposa su cuerpo en una fosa común junto a 15 mujeres más.

Una anécdota que se cuenta de ella –no sabemos si verdadera- es que era sonámbula y algunas noches dejaba sobre la mesa un problema sin resolver. Cuando se levantaba por la mañana, el problema estaba resuelto: al parecer ¡¡mientras dormía lo había resuelto!!

La hemos traído aquí por su contribución y avance al estudio y divulgación de Matemáticas, aunque desde la muerte de su padre y roto, por lo tanto su compromiso, parece que las matemáticas pasan a segundo plano. Más bien las estuvo tratando como entretenimiento o un simple pasatiempo. ¡Cuánto hubiese avanzado si lo hubiese tomado como su actividad principal!

Su contacto con la familia Ricatti ejerce tal influencia sobre ella que la empujan a la edición y publicación de Instituzioni analitiche ad uso della gioventu italiana. Este libro, en dos tomos, es considerado el primer libro de texto, incardinando en una secuencia lógica todos los conocimientos matemáticos, hasta entonces, que permanecían dispersos por libros y manuales de todo tipo; crea el texto completo que estudia y enlaza de manera lógica tanto el cálculo diferencial e integral como las ecuaciones diferenciales y la geometría y el álgebra, así como toda la notación y simbología matemática, que se utiliza hasta nuestros días. La concisión, la claridad y la minuciosidad de todo su estudio son asombrosas, aunque es normal que tuviese algunas lagunas, que afloraban sus críticos. En 1775 se publica en Paris la edición francesa y la edición inglesa en 1801.

Pertenece, por mérito propio, a la historia de las Matemáticas, pero es más conocida por la curva: la bruja de Agnesi, que ya había sido estudiada por Fermat en 1703 y había sido representada y construida en 1718 por Grandi. Ella la introdujo en su famoso libro y ello la catapultó a la fama. Pero ¿de dónde proviene lo de bruja? Veamos. Grandi llamó a la curva versoria, en latín; y versiera en italiano, que significa cuerda que hacer girar la vela (en un barco). Agnesi escribió de la curva llamándola la versiera (le puso el artículo). Su traductor en la edición inglesa (John Colson) le llama witch (la bruja, ¡¡quizás pudo ser una broma del traductor!!) porque confunde, dado su poco conocimiento del italiano versiera por avversiera (que significa “demonia” o bruja). Así que ya tenemos el entuerto. El idioma español traduce del inglés La bruja, y ya, nuestra curva, se quedó con su apodo, para el resto de los días. La verdad es que es curiosa la historia, pero las historias de la historia de la ciencia tienen, a veces, entramados como este. La curva es:

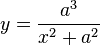
Representa a una curva con asíntota horizontal el eje OX y que tiene su máximo en x=0, es decir (0,a), que puede verse y construirse en Geogebra.org. La gráfica es: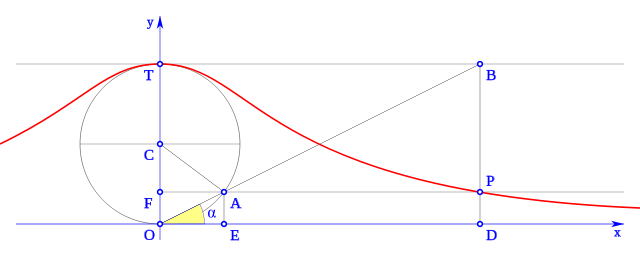

Durante la Edad Media en muchos países europeos la educación superior para las mujeres fue tratada con una oposición furibunda: fueron privadas de los cauces fundamentales del aprendizaje de las enseñanzas superiores, que se circunscribía, prácticamente, a conventos y monasterios. Tras la caída de Constantinopla, los científicos y eruditos llegan y se instalan en Roma y la aceptación de la mujer va progresando en Italia y en resto de Europa (aunque más lentamente).

En Italia, con la llegada del Renacimiento, la mujer tiene acceso al mundo académico, sin apenas cortapisas. Las italianas participan en todas las ramas de las Artes y las Ciencias. Esta apertura tardó bastante tiempo en llegar a las naciones europeas próximas.

Estos avances “feministas” (¡si podemos llamarles así!) en Italia posibilitaron el ingreso de María en la Academia de las Ciencias de Bolonia, de Italia, pero no en la de Francia donde el secretario de la Comisión que le denegó la entrada dijo de su obra:”….No conozco ningún trabajo de este tipo que sea más claro, más metódico o más completo que sus Instituciones analíticas. No hay ninguno en ningún idioma que pueda guiar de manera más segura, conducir con mayor rapidez y llevar más adelante a quienes desean avanzar en las ciencias matemáticas. Admiro en particular el arte con el que reúne usted bajo métodos uniformes las distintas conclusiones dispersas en las obras de los geómetras, y a las que han llegado por métodos diferentes”. Pero incluso con estos elogios ¡la dejaron fuera!

Su figura fue reivindicada en Italia mucho tiempo después. Un siglo más tarde se pusieron nombres de calles y plazas en toda Italia: Milán, Roma, Monza,…; se crearon becas que llevan su nombre; fundaciones,.. Para ver más sobre su biografía y su obra en Wikipedia, divulgamat, gaussianos, y Google docs.com.

Otra mujer que tuvo que luchar contra el machismo imperante, y aunque que tuvo que hacer frente a las cuestiones hogareñas, sobrevenidas involuntariamente, su talento e inteligencia permitieron integrar todos los conocimientos matemáticos en esa fecha en un libro de texto y posibilitaron que fuese una mujer matemática, que ocupa por mérito propio un lugar en la historia de esta Ciencia. AMJ

Sophie Germain, la matemática obstinada: de la persistencia al éxito.

Traíamos recientemente en una entrada (Mersenne y sus primos) las noticias y avances producidos últimamente en la teoría de los números primos: el descubrimiento del mayor número primo conocido, el M48; y hoy traemos aquí a una matemática que profundizó extraordinariamente en la teoría de números -su pasión- y, en particular, en el estudio de los números primos. Se trata de Sophie Germain, que ante las dificultades a las que se enfrentó en su vida – por ser mujer, fundamentalmente- siempre lo hizo con valentía y perseverancia. Gracias a ello ha formado parte de la Historia de las Matemáticas. Su lucha contra la misoginia imperante en aquellos tiempos es digna de ser recordada. Pasamos a contar su azarosa vida y su contribución al avance de la Ciencia.

Nació en Paris (1 de Abril de 1776) en el seno una familia acomodada, pero no de la aristocracia –su padre era un comerciante burgués y liberal que llegó a ser diputado en la Asamblea Nacional y más tarde director del Banco de Francia-, poseedora de una vasta biblioteca, que aprovechó considerablemente a partir de su adolescencia. Hizo de la lectura y el estudio- desde los 13 años- su actividad predilecta y casi única. Algunos autores afirman que en ese tiempo fue confinada en casa debido a la instauración de la Revolución Francesa. Para leer a Newton y Euler necesitaba aprender latín, cuestión que hizo en poco tiempo. Cuando fue descubierta su inclinación por ese tipo de lectura y estudio su familia decidió impedírselo de cualquier manera. Fue imposible persuadirle de abandonarlos. Llegaron incluso a dejarla sin luz y sin calefacción. Pero no sabían de la tenacidad y la testarudez de la damisela.La muchacha, a escondidas, se envolvía en una manta y con la luz de una vela –que sisaba- se sumergía en el mundo fascinante de las matemáticas. Así hasta que fue descubierta y entonces supieron que jamás doblegarían a la obstinación de una feminista en el siglo XVIII.

Pero también sabían que, aunque le permitieran proseguir sus estudios científicos, no iba a obtener sus aspiraciones y pretensiones y que tampoco, como mujer, iba a conseguir los objetivos femeninos de ese tiempo que le tocó vivir (boda, maternidad,…). Recordemos que estamos a finales del siglo XVIII y hasta 1972(¡¡sí, sí, hasta 1972!!) las mujeres no pudieron matricularse en la Escuela Politécnica de París (fundada en1794 con la intención de que los matemáticos franceses no abandonaran el país). Su estudio, por lo tanto, estaba “casi prohibido” por la fuerza de la costumbre y el machismo reinante, incluso en una Francia revolucionaria. Nada de esto la frenó, si bien su padre le financió sus proyectos e investigaciones, único estímulo que recibió en toda su vida.

A través de un amigo de la familia consiguió los apuntes de las enseñanzas de Lagrange - tuvo la suerte de vivir en el gran siglo de las matemáticas francesas- al que le hacía llegar- con seudónimo- sus reflexiones. Ante la profundidad de sus trabajos Lagrange la aceptó, encantado y sorprendido a la vez, convirtiéndose en su mentor, amigo y profesor, haciéndole participar en sus tertulias científicas. Sin embargo al no haber seguido una enseñanza reglada – más bien desorganizada y anárquica- , las lagunas en su formación matemática eran palpables e impidieron así una mayor altura de sus avances.

Mantenía correspondencia con Gauss- probablemente uno de los matemáticos más brillantes que haya existido-, sobre todo después de leer la obra de éste: Disquisiciones aritméticas; obra que abrió la espita de su pasión: la Teoría de números. Y dentro de sus anhelos, la conjetura de Fermat fue la reina de sus obsesiones. El Teorema de Germain es el mayor avance en la resolución de dicho problema en los dos últimos siglos. Era tal el respeto y admiración por el gran Gauss que se dirige a él en la siguiente forma: "Por desgracia, la profundidad de mi intelecto no se corresponde con la voracidad de mi apetito, y me parece ciertamente una osadía importunar a un hombre de genio cuando yo no merezco su atención más que por la admiración que le profeso y que sin duda comparto con todos sus lectores".

De adolescente le impactó la noticia de la muerte de Arquímedes a manos de un soldado romano. –el libro Historia de las Matemáticas de Jean-Etienne Montucla estuvo durante tiempo en la cabecera de su cama-, así que cuando Napoleón ocupa Alemania -Prusia- ella intercede a favor de Gauss al tener noticia que el ejército francés invade Brunswick –ciudad natal de Gauss-; éste al enterarse que su “protectora” es femenina y que era quien se carteaba con ella (hasta entonces usaba el pseudónimo de Sr. Le Blanc) le escribió lo siguiente:

“Pero cómo describirte mi admiración y asombro al ver que mi estimado corresponsal Sr. Le Blanc se metamorfosea en este personaje ilustre que me ofrece un ejemplo tan brillante de lo que sería difícil de creer. La afinidad por las ciencias abstractas en general y sobre todo por los misterios de los números es demasiado rara: lo que no me asombra ya que los encantos de esta ciencia sublime sólo se revelan a aquellos que tienen el valor de profundizar en ella. Pero cuando una persona del sexo que, según nuestras costumbres y prejuicios, debe encontrar muchísimas más dificultades que los hombres para familiarizarse con estos espinosos estudios, y sin embargo tiene éxito al sortear los obstáculos y penetrar en las zonas más oscuras de ellos, entonces sin duda esa persona debe tener el valor más noble, el talento más extraordinario y un genio superior”.

Nadie mejor que Gauss lo puede decir tan claro y tan alto: un talento extraordinario y un genio superior. ¡Qué hubiese sido de Sophie con una educación matemática apropiada a su valía!

Su tenacidad fue una constante en su vida. Tuvo que presentar su trabajo hasta tres veces a la Academia Francesa de la Ciencia en Paris para que le concedieran una Medalla de Oro, por su trabajo Mémoire sur les Vibrations des Surfaces Élastiques. Su rival en el tema de la Elasticidad era Poisson, que también era juez del concurso. Consecuencia: falta de reconocimiento público y científico de sus progresos en la materia. “Simplemente las mujeres no eran tomadas en serio”, aunque fue la primera mujer invitada a participar en las sesiones de la Academia de la Ciencia.

Hasta su muerte siguió trabajando en Matemáticas y en Filosofía. Incluso fue elogiada por Comte por el ensayo filosófico: Considérations générales sur l’état des Sciencies et des lettres.

Murió de cáncer de mama en Paris, el 27 de Junio de 1831, cuando estaba en la cima de su producción matemática y científica -acababa de publicar sus últimos artículos sobre teoría de números y curvatura de superficies- y además no pudo disfrutar del título honorifico que le propuso la Universidad de Gottingen, inducida por el propio Carl F. Gauss.

Nosotros hemos traído aquí a Sophie Germain, fundamentalmente, por sus avances en la Teoría de Números, cuestión que pasamos a tratar.

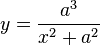
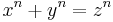Lo que sedujo a Sophie Germain de la Teoría de Números fue que enunciados tan simples llevaran tanto siglos sin encontrar soluciones para ellos. Dirigió su dedicación hacia el último Teorema de Fermat (Si n es un número entero mayor que 2, entonces no existen números enteros x, y y z, tales que se cumpla la igualdad: , demostrado finalmente en 1995 por Andrew Wiles).

En una carta dirigida a Gauss en 1808 le comunica su resultado más brillante: Si x, y, z son números enteros, tales que x⁵+y⁵+z⁵=0 entonces, al menos uno de los números x, y o z debe ser divisible por 5. La generalización de este resultado es el que en el futuro sería el teorema que lleva su nombre.

El teorema de Sophie Germain dice que si n es un número primo y 2n+1 también es primo, entonces el primer caso del teorema de Fermat es verdadero (cuando ninguno de los tres números es divisible por n). A esos números terminaron llamándoles números primos de Sophie Germain y forman una sucesión 2, 3, 5, 11, 23,28,…….

Este resultado es el más importante desde que Fermat en 1736 estableció su conjetura hasta los avances de Kummer en 1940.

Ver más en history-mcs; luna-sierra.org; historias de la ciencia; divulgamat2; pagina12.com; agnesscot.com; y en los muy buenos enlaces pbs.org. y la enciclopedia.com.

Para los franceses es, casi con toda seguridad, la mujer con mayor altura intelectual y científica de su historia, junto a Émilie du Châtelet. Se interesó no sólo por las Matemáticas y la Física; también por la Filosofía, la Química, la Geografía y la Historia. Incluso, hoy día, estudiosos de sus manuscritos apuntan a que en ellos hay bastante más de lo que parece; urge por tanto revisarlos. Fue honrada de distintas maneras –pero nunca como se merecía-: una calle en París, una escuela también en París y la casa donde murió fue convertida en monumento histórico, el Instituto de Francia concede anualmente el premio “ Le prix Sophie Germain” al investigador en Matemáticas más sobresaliente,entre otros.

Sin embargo la colección de “feos” a lo largo de su vida no paró ni después de su muerte: al construir la Torre Eiffel fueron incluidos los nombres de los setenta y dos sabios (ingenieros y cientificos) franceses más importantes (¡¡¡todos varones!!!!) no aparecía el nombre de Sophie Germain, que casualmente contribuyó a los avances de la ¡¡¡teoría de la elasticidad de los metales!!! Desde entonces hasta hoy la situación de la mujer en la ciencia ha cambiado mucho, muchísimo, pero todavía no al mismo nivel , según que países. Leemos por algún foro: “ es difícil ser mujer en el mundo de la ciencia”. Todavía deben seguir cambiando los modos y los modelos para que los desprecios por la capacidad intelectual femenina sea, sólo, un mal recuerdo del pasado. ¡Pero que muy pasado! AMJ

Émilie du Châtelet, las Matemáticas y los placeres terrenales.

Un 17 de Diciembre de 1706 nació en Paris la que es considerada la primera gran científica y matemática francesa Émilie du Châtelet. Hija del jefe de protocolo de Luis XIV, desde pequeña, se prodigaba en demostrar su inteligencia y conocimientos por doquier. Era tal su interés por el estudio, algo impropio de la época al tratarse de una niña, que desde los seis años estudiaba latín y griego, en su domicilio educada por instructores particulares, algo común en la época en familias de alta alcurnia y en particular en aquellas donde las inquietudes culturales eran “moneda común”. Estudió también matemáticas, latín y griego, física, música e inglés, entre otras actividades deportivas y culturales; pero su preferida era las Matemáticas.

A los 16 años fue presentada en sociedad: en la corte de Versalles. Desde entonces sus correrías, extravagancias y sobre todo su glamour fueron exaltados a la máxima potencia: disfrutó hasta el límite de lo permitido a una mujer en esos tiempos, y en más de una ocasión traspasó ese límite. A los 19 años se casó con el militar marqués du Châtelet, con el que tuvo dos hijos en los dos primeros años de matrimonio y otra que murió fruto de amoríos con el poeta Saint-Lambert. Parece que el matrimonio le hizo sentar la cabeza -y a su vez subir de posición social llegando a la nobleza militar-, pero siempre fue una mujer adelantada a su tiempo, también en costumbres sociales y comportamientos fuera de lo común.

Una vida socialmente intensa traía una conducta libertina y amoríos diversos: su reputación de frívola no era equivocada. La aristocracia, a la que ella pertenecía, puso de moda el estudio de la Ciencia y los nuevos descubrimientos. Ella, por lo tanto, siguió el camino de los de su clase: se dedicó a la ciencia y a las tertulias en los cafés de Paris, donde estaba prohibida la entrada de mujeres. Para ello se disfrazó alguna vez – desafiando costumbres y normas- y participaba así de reuniones, charlas y debates sobre filosofía, ciencia, política, poesía,… lo que cayera por el lugar. Participaba así de las noches bohemias de Paris y de sus juergas correspondientes.

Sus conocimientos de la lengua inglesa le permitieron traducir a Locke y a Newton y participar, consecuentemente, en debates científicos y filosóficos. Para ello debió aumentar sus conocimientos científicos y matemáticos, para entender totalmente los documentos que traducía. Se rodeó de matemáticos seguidores de Newton como Maupertuis y Clairaut(¡que a la postre fueron amantes suyos!) y el alemán Koening –alumno de Leibniz- y con su ayuda el nivel científico de la marquesa fue el óptimo para sus propósitos y objetivos. La investigación le exigía demasiado tiempo, que escasamente podía disponer, lo que le frustraba enormemente. De todas formas su obra escrita es abundante en matemáticas, filosofía- metafísica- , religión y lengua.

Portada de Les Élements de la Philosophie de Newton de Voltaire, donde Émilie Du Châtelet aparece como su musa inspiradora

En 1734 tras la orden de arresto contra Voltaire a causa de la edición de las cartas inglesas sin permiso, Émilie le ofreció como refugio su castillo de Cirey, en el norte de Francia, que más tarde convirtieron en su nido de amor y de estudio.

Este tiempo de soledad les apartó de la corte, pero su producción científica lo compensó y, sobre todo, su relación personal muy intensa; y aunque su marido también pasaba temporadas en el castillo, el temor al escándalo le hizo aceptar la situación (otros autores dan la versión de los préstamos de Voltaire para la reconstrucción del castillo y los gastos de su estancia). Lo cierto es que ella “disfrutaba de lo lindo” y su marido “cornudo consentido”. A partir de 1739 comenzaron de nuevo sus estancias en Paris y sus viajes a Bruselas, Luneville,…

La edad de su amante (¡ya no le servía para sus juegos eróticos!) y la inclinación de ella al juego de naipes (¡a punto estuvo de arruinarla en varias ocasiones!) fueron enfriando el amor en la pareja. En 1745 rompió la relación con Voltaire, pero siguieron viviendo juntos hasta su muerte. Más tarde se enamoró de Saint-Lambert, poeta y militar, bastante más joven que ella (¡era lo que buscaba y necesitaba!), del que quedó embarazada y, a la postre, como consecuencias del parto murió, trabajando hasta el mismo día de su muerte. Pero murió joven, el 10 de Septiembre de 1749, a los 43 años, y ello limitó por tanto su producción científica.

Tradujo algunas obras de Newton, como Essais sur l’optique , Institutions de Physique , o el más famoso Principia Mathematica. Intentó ser autónoma en su pensamiento lo que le trajo no pocos sinsabores y disgustos, sobre todo con Voltaire y después con su amigo Koening, con quien al darle un estudio para pedirle opinión éste se apropió del resultado: restableció la autoría sobre sus trabajos un tiempo después. La Sorbonne llego a reconocer sus avances, así como algunos de sus contemporáneos.

(Pg. de su cuaderno).

Incluso la Academia de Ciencias de Bolonia la admitió en 1746. Su insistencia en escribir en secreto parece que se fundamenta en dos pilares: su condición de mujer y sus planteamientos novedosos y ambas cosas unidas aumentaba el riesgo. Tuvo tiempo de terminar de traducir Principies mathematiques de la philosofie de Newton, pero lo publicó su amigo y amante Voltaire, ya en 1752, reconociendo en su prefacio la fortaleza de la científica en sus últimos días, que pasó junto a ella.

La única mujer francesa, de su tiempo, que dedicó seriamente su talento a las matemáticas y a la física, y ¡la primera que tradujo a Newton del latín! Más en Wikipedia , matpages.com, history-mcs, visitvoltaire.com" love story",o en Portalplaneta.com. Enlace para la película "Divine Emilie"(2007).

Como dice de ella Fernando Savater en un estupendo artículo en El País “…se dedicó a la filosofía y no al prejuicio, a la ciencia y no a la superstición, a la pasión y no a la gazmoñería, al juego y no a la oración, a la felicidad y no al renunciamiento. No se entregó al confesor ni a la familia, sino a Voltaire. Y cuando años después comprobó que el enciclopedista, además de descuidarla por otras, ya flaqueaba a la hora sagrada del empuje erótico, se buscó un amante joven y vigoroso, incluso demasiado vigoroso quizás. Hizo bien, que caramba: chapeau!...”

Fue pionera en estos comportamientos, abiertamente contrarios a la moral dominante y a las convenciones sociales establecidas: libre y culta, por encima de todo. Y una sed insaciable de conocimiento, saber, cultura y amor. Su Discurso sobre la felicidad debe formar parte de la mesita de noche de todo aquel que quiera conocerla y su pasión por la vida y por la ciencia.

ISBN: 9788437625232

Su vida, en fin, feliz y desdichada, libre por encima de todo y gozosa de “casi” todos los placeres de esta vida .AMJ

Ada Lovelace, la madre de la Informática.

Un día como hoy, 10 de Diciembre, pero de 1815 nació la matemática londinense Augusta Ada King, Condesa de Lovelace, y más conocida como Ada Lovelace. Es considerada como la primera programadora, escribiendo símbolos y algoritmos para la máquina de Babbage, que todavía no había sido construida, aunque sí perfilada por el profesor de matemáticas, también inglés, Charles Babbage.

Era hija del famoso poeta Lord Byron, pero como “en casa del herrero cuchillo de palo”, no se le conoce ningún poema o texto dignos de ser tenidos en cuenta. La relación tormentosa de sus padres llevó a su madre, Annabella Milbanke, a alejar a su hija todo lo posible de la poesía y desterrar así cualquier posible inclinación de la niña por ese "mundillo": cualquier parecido con su padre, en cuanto a su "modus vivendi", había que eliminarlo. Rodeó por lo tanto a su hija de excelentes profesores de Matemáticas, que la condujeron por un mundo bastante avanzado, científicamente, para las mujeres de esa época. De todos modos su padre murió cuando ella tenía 8 años, después de haber llevado una vida bastante convulsa (líos amorosos con una hermanastra que le obligaron a abandonar Inglaterra, precipitadamente), y en tan poco tiempo su influencia hubo de ser pequeña.

Mary Somerville se convirtió en su tutora y Ada se refugió, así, en la Ciencia y en lo que sí sobresalió fue en Matemáticas, y eso que su vida fue bastante corta: murió cuando tenía 36 años -la misma edad a la que murió su padre-, debido a un cáncer de útero y sobre todo a la medicina empleada para ello (las sangrías típicas de la época).

Al principio se dedicó a trabajar en dos teorías muy en boga en aquellos tiempos: el mesmerismo y la frenología; la primera como el estudio del magnetismo en algunos animales y la segunda como la teoría de conocer el comportamiento a través de su aspecto fisiológico, lo que ayudó a resolver algunos crímenes. Pero no era ese su destino: eran los números, las funciones, los algoritmos,… la ahora llamada informática. Durante mucho tiempo se creyó que la aportación de Lovelace a la programación era sólo como traductora de Babbage pero últimamente se sabe que fue la primera persona en describir un lenguaje de programación, tal como se entiende hoy, y se le reconocen sus aportaciones e ideas originales. Puede considerársele como la madre de la programación informática.

Escribió un programa sobre los números de Bernoulli e incluso uno sobre valores trigonométricos. Igualmente sugirió que las instrucciones e información para la máquina se hiciesen por tarjetas perforadas e inició una nueva notación para la escritura de los programas informáticos.

No fueron reconocidas en vida sus aportaciones, fundamentales, aunque sí después de su muerte. Ya en el siglo XX sí fueron utilizados sus avances informáticos. En su honor se llamó lenguaje de programación Ada por el Ministerio de Defensa de EEUU a uno de finales del siglo XX. En 2010 se empieza a rodar una película sobre ella: “La encantadora de números”.

La vida de los números ha sido a lo largo de la Historia eminentemente masculina: incluso tuvo que firmar con iniciales algunos de sus avances matemáticos. Más noticias en ABC, La Voz de Galicia y Cadena Ser.

Se casó con 20 años y siguió investigando, y aunque tuvo tres hijos, al final fue "repudiada" por su marido(¡quizás una infidelidad!); la influencia de su madre fue decisiva en toda su vida y le "debe" su dedicación a estos menesteres investigadores y a la aversión a la poesía de su progenitora.

Google le homenajea hoy y le ha dedicado un doodle. Una de las mujeres que a lo largo de la Historia de la Ciencia más ha contribuido a sus avances y desarrollo. AMJ.

Florence Nightingale: la enfermera y la Estadística.

El 12 de mayo de 1820 nació en Florencia , aunque británica, F. Nightingale.Y vivió 90 años. En su efemérides la recordamos. ¿Pero quién era?. Pues una de las primeras mujeres que se dedicaran a la enfermería y considerada como la madre de la enfermería moderna. Sus libros tuvieron muchísima repercusión en la sanidad militar, los hospitales, las asistencias a enfermos, etc. Se dedicó a promover su profesión y fundó una Escuela de Enfermería que lleva su nombre y en este día de su nacimiento se debe el día Mundial de la Enfermera. En algunos hospitales redujo la mortalidad desde el 40% al 2%. Además la educación formó parte de toda su vida, fundamentalmente en el campo de la enfermería. Pero ¿por qué la traemos aquí, a este blog matemático?. Pues porque sus estudios estadísticos fueron muy avanzados para su época, y que ahora intentaremos enumerar.

En 1860 fue la primera mujer que formó parte de la Royal Statistical Society, fundamentalmente por sus estudios estadísticos sobre mortalidad en la guerra de Crimea y la mala gestión de los hospitales de campaña. Junto con Galton intentó crear una cátedra de Estadística en Oxford pero fracasó porque no compartían desde la Universidad el interés por aplicar la estadística a las ciencias y problemas sociales. Fue pionera en la presentación gráfica de los resultados estadísticos, como histogramas y gráficos de sectores. Igualmente fue innovadora en la tabulación y recogida de datos en la estadística descriptiva, y lo utilizó todo para controlar y mejorar la práctica médica. Desarrolló una fórmula modelo de estadística hospitalaria para generar datos hospitalarios consistentes.

Evidentemente fue una adelantada a su tiempo y feminista sin lugar a dudas, y se mantuvo firme en sus ideas y postulados ante una sociedad que se oponía a que la mujer ocupara puestos distintos para los que "había sido destinada", comenzando por su propia familia.

(En la lámina del comienzo se observa un ejemplo de diagrama polar)

Sobre su vida, obras y demás, con cierta profundidad, se puede consultar en los enlaces siguientes: Wikipedia, ibe.unesco y página de su museo de Londres.  La BBC en 2009 dramatizó un documental sobre su vida:

AMJ

Emmy Noether(1882-14 de Abril de 1935)- Otra científica perseguida.

Traemos aquí a otra científica, física y matemática, perseguida, como otras muchas, en este caso por su condición de mujer y judía. Es conocida por su contribución al desarrollo del álgebra abstracta y la física teórica. Un 14 de Abril de 1935(que en España celebramos la efemérides de la proclamación de la II República, aunque en 1931) murió después de ser intervenida de un tumor ovárico.

Algunos trazos de su vida son los que siguen: Nació en Baviera en 1882, y su padre también era matemático; pensaba dedicarse a enseñar idiomas pero, afortunadamente, cambió de idea y estudió Matemáticas en Nuremberg y trabajó, sin cobrar, durante siete años en Erlangen. Fue invitada por Hilbert y Klein a unirse al centro de investigación matemática de la Universidad de Notinga, donde estuvo hasta 1933, habiendo publicado junto al holandés Van der Waerden en 1931 Álgebra moderna. En los años siguientes el gobierno nazi alemán expulsó a los judíos de los puestos docentes de la Universidad y, por lo tanto, emigró a los Estados Unidos, donde recaló en Princenton(Pensilvania), donde coincidió con Einstein.

En Matemáticas Noether contribuyó extraordinariamente a la teoría de los invariantes y de los cuerpos numéricos; la teoría de los ideales en los anillos conmutativos y también publicó obras fundamentales sobre álgebras conmutativas y números hipercomplejos. Se le reconocen también trabajos muy importantes en topología algebraica. Para más profundidad sobre su biografía se puede consultar su biografía en : http://es.wikipedia.org/wiki/Emmy_Noether

o también en http://www.fmujeresprogresistas.org/fichavisibilidad/Noether.htm

En el vídeo del principio repasamos su vida y su obra.

La editorial Nivola en su colección La matemática en sus personajes publica un libro sobre su vida, su contribución a la ciencia y su influencia en la matemática de su tiempo; y sobre todo es por su discriminación por ser mujer ( trabajar sin remuneración) y judía( fue expulsada de la Universidad) por lo que más se le valora su contribución a la ciencia y por lo que aquí la distinguimos.

Emmy Noether. Una matemática ideal David Blanco Laserna ISBN: 978-84-92493-79-1 256 páginas
AMJ

Sofía Kovalevskaya

Hoy 10 de Febrero se cumplen 120 años de la muerte de la matemática rusa Sofía Kovalesvskaya.Ella es la primera mujer en el mundo que obtuvo un doctorado en Matemáticas ,en 1874 en la Universidad de Göttingen y también la primera mujer que obtuvo plaza de profesora universitaria en esa misma Universidad. Era descendiente de Corvino, rey de Hungría, pero su abuelo por casarse con una gitana perdió el título de príncipe.

A las mujeres se les impedía el acceso a la Universidad; por lo que, para escapar del control paterno se casó con Kovalevski, pero incluso así tampoco la dejaron acceder y terminó en Berlín, trabajando en privado con Weirstrass, el mejor matemático de la época. Murió a los 41 años de gripe. Para estudiar más datos sobre su vida consultar: http://es.wikipedia.org/wiki/Sofia_Koval%C3%A9vskaya

o en http://mujeresriot.webcindario.com/Kovalevskaya.htm .O también en http://www.uv.mx/cienciahombre/revistae/vol23num3/articulos/kovalevskaya/index.html

Trabajó en ecuaciones en derivadas parciales e integrales abelianas. Su trabajo ha dado resultados como la mecánica de la astronomía (trabajo en los anillos de Saturno, en particular). En 1888 logró el prestigoso Premio Bordin de Matemáticas, siendo la primera mujer que lo lograba, para lo cual tuvo que resolver las célebres Ecuaciones de Euler "sobre la rotación de un sólido pesado alrededor de un punto fijo", un problema que desde hacía muchos años traía de cabeza a los mejores matemáticos.
Como cita quedará la de

"No es posible ser matemático sin llevar un poeta en el alma"

El poeta debe ser capaz de ver lo que los demás no ven,
debe ver más profundamente que otras personas.
Y el matemático debe hacer lo mismo.

Fue una mujer extraordinaria tanto en el aspecto científico como en su forma de entender la vida. Era una mujer de ideas nihilistas, fundó revistas, escribió libros, luchó por la causa de la mujer, tuvo una hija.... Fue discriminada por ser mujer y quizás por ser de etnia gitana, pero no se rindió nunca.En fin, una luchadora.