Sophie Germain, la matemática obstinada: de la persistencia al éxito.
Traíamos recientemente en una entrada (Mersenne y sus primos) las noticias y avances producidos últimamente en la teoría de los números primos: el descubrimiento del mayor número primo conocido, el M48; y hoy traemos aquí a una matemática que profundizó extraordinariamente en la teoría de números -su pasión- y, en particular, en el estudio de los números primos. Se trata de Sophie Germain, que ante las dificultades a las que se enfrentó en su vida – por ser mujer, fundamentalmente- siempre lo hizo con valentía y perseverancia. Gracias a ello ha formado parte de la Historia de las Matemáticas. Su lucha contra la misoginia imperante en aquellos tiempos es digna de ser recordada. Pasamos a contar su azarosa vida y su contribución al avance de la Ciencia.
Nació en Paris (1 de Abril de 1776) en el seno una familia acomodada, pero no de la aristocracia –su padre era un comerciante burgués y liberal que llegó a ser diputado en la Asamblea Nacional y más tarde director del Banco de Francia-, poseedora de una vasta biblioteca, que aprovechó considerablemente a partir de su adolescencia. Hizo de la lectura y el estudio- desde los 13 años- su actividad predilecta y casi única. Algunos autores afirman que en ese tiempo fue confinada en casa debido a la instauración de la Revolución Francesa. Para leer a Newton y Euler necesitaba aprender latín, cuestión que hizo en poco tiempo. Cuando fue descubierta su inclinación por ese tipo de lectura y estudio su familia decidió impedírselo de cualquier manera. Fue imposible persuadirle de abandonarlos. Llegaron incluso a dejarla sin luz y sin calefacción. Pero no sabían de la tenacidad y la testarudez de la damisela.La muchacha, a escondidas, se envolvía en una manta y con la luz de una vela –que sisaba- se sumergía en el mundo fascinante de las matemáticas. Así hasta que fue descubierta y entonces supieron que jamás doblegarían a la obstinación de una feminista en el siglo XVIII.
Pero también sabían que, aunque le permitieran proseguir sus estudios científicos, no iba a obtener sus aspiraciones y pretensiones y que tampoco, como mujer, iba a conseguir los objetivos femeninos de ese tiempo que le tocó vivir (boda, maternidad,…). Recordemos que estamos a finales del siglo XVIII y hasta 1972(¡¡sí, sí, hasta 1972!!) las mujeres no pudieron matricularse en la Escuela Politécnica de París (fundada en1794 con la intención de que los matemáticos franceses no abandonaran el país). Su estudio, por lo tanto, estaba “casi prohibido” por la fuerza de la costumbre y el machismo reinante, incluso en una Francia revolucionaria. Nada de esto la frenó, si bien su padre le financió sus proyectos e investigaciones, único estímulo que recibió en toda su vida.
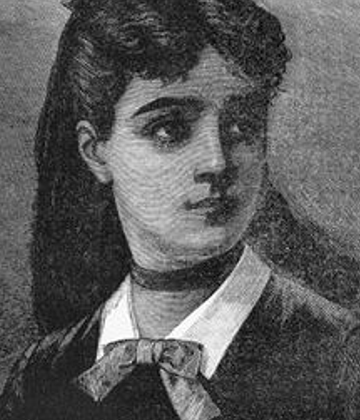
A través de un amigo de la familia consiguió los apuntes de las enseñanzas de Lagrange - tuvo la suerte de vivir en el gran siglo de las matemáticas francesas- al que le hacía llegar- con seudónimo- sus reflexiones. Ante la profundidad de sus trabajos Lagrange la aceptó, encantado y sorprendido a la vez, convirtiéndose en su mentor, amigo y profesor, haciéndole participar en sus tertulias científicas. Sin embargo al no haber seguido una enseñanza reglada – más bien desorganizada y anárquica- , las lagunas en su formación matemática eran palpables e impidieron así una mayor altura de sus avances.
Mantenía correspondencia con Gauss- probablemente uno de los matemáticos más brillantes que haya existido-, sobre todo después de leer la obra de éste: Disquisiciones aritméticas; obra que abrió la espita de su pasión: la Teoría de números. Y dentro de sus anhelos, la conjetura de Fermat fue la reina de sus obsesiones. El Teorema de Germain es el mayor avance en la resolución de dicho problema en los dos últimos siglos. Era tal el respeto y admiración por el gran Gauss que se dirige a él en la siguiente forma: "Por desgracia, la profundidad de mi intelecto no se corresponde con la voracidad de mi apetito, y me parece ciertamente una osadía importunar a un hombre de genio cuando yo no merezco su atención más que por la admiración que le profeso y que sin duda comparto con todos sus lectores".
De adolescente le impactó la noticia de la muerte de Arquímedes a manos de un soldado romano. –el libro Historia de las Matemáticas de Jean-Etienne Montucla estuvo durante tiempo en la cabecera de su cama-, así que cuando Napoleón ocupa Alemania -Prusia- ella intercede a favor de Gauss al tener noticia que el ejército francés invade Brunswick –ciudad natal de Gauss-; éste al enterarse que su “protectora” es femenina y que era quien se carteaba con ella (hasta entonces usaba el pseudónimo de Sr. Le Blanc) le escribió lo siguiente:
“Pero cómo describirte mi admiración y asombro al ver que mi estimado corresponsal Sr. Le Blanc se metamorfosea en este personaje ilustre que me ofrece un ejemplo tan brillante de lo que sería difícil de creer. La afinidad por las ciencias abstractas en general y sobre todo por los misterios de los números es demasiado rara: lo que no me asombra ya que los encantos de esta ciencia sublime sólo se revelan a aquellos que tienen el valor de profundizar en ella. Pero cuando una persona del sexo que, según nuestras costumbres y prejuicios, debe encontrar muchísimas más dificultades que los hombres para familiarizarse con estos espinosos estudios, y sin embargo tiene éxito al sortear los obstáculos y penetrar en las zonas más oscuras de ellos, entonces sin duda esa persona debe tener el valor más noble, el talento más extraordinario y un genio superior”.
Nadie mejor que Gauss lo puede decir tan claro y tan alto: un talento extraordinario y un genio superior. ¡Qué hubiese sido de Sophie con una educación matemática apropiada a su valía!
Su tenacidad fue una constante en su vida. Tuvo que presentar su trabajo hasta tres veces a la Academia Francesa de la Ciencia en Paris para que le concedieran una Medalla de Oro, por su trabajo Mémoire sur les Vibrations des Surfaces Élastiques. Su rival en el tema de la Elasticidad era Poisson, que también era juez del concurso. Consecuencia: falta de reconocimiento público y científico de sus progresos en la materia. “Simplemente las mujeres no eran tomadas en serio”, aunque fue la primera mujer invitada a participar en las sesiones de la Academia de la Ciencia.
Hasta su muerte siguió trabajando en Matemáticas y en Filosofía. Incluso fue elogiada por Comte por el ensayo filosófico: Considérations générales sur l’état des Sciencies et des lettres.
Murió de cáncer de mama en Paris, el 27 de Junio de 1831, cuando estaba en la cima de su producción matemática y científica -acababa de publicar sus últimos artículos sobre teoría de números y curvatura de superficies- y además no pudo disfrutar del título honorifico que le propuso la Universidad de Gottingen, inducida por el propio Carl F. Gauss.
Nosotros hemos traído aquí a Sophie Germain, fundamentalmente, por sus avances en la Teoría de Números, cuestión que pasamos a tratar.
Lo que sedujo a Sophie Germain de la Teoría de Números fue que enunciados tan simples llevaran tanto siglos sin encontrar soluciones para ellos. Dirigió su dedicación hacia el último Teorema de Fermat (Si n es un número entero mayor que 2, entonces no existen números enteros x, y y z, tales que se cumpla la igualdad: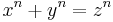 
, demostrado finalmente en 1995 por Andrew Wiles).
En una carta dirigida a Gauss en 1808 le comunica su resultado más brillante: Si x, y, z son números enteros, tales que x5+y5+z5=0 entonces, al menos uno de los números x, y o z debe ser divisible por 5. La generalización de este resultado es el que en el futuro sería el teorema que lleva su nombre.
El teorema de Sophie Germain dice que si n es un número primo y 2n+1 también es primo, entonces el primer caso del teorema de Fermat es verdadero (cuando ninguno de los tres números es divisible por n). A esos números terminaron llamándoles números primos de Sophie Germain y forman una sucesión 2, 3, 5, 11, 23,28,…….
Este resultado es el más importante desde que Fermat en 1736 estableció su conjetura hasta los avances de Kummer en 1940.
Ver más en history-mcs; luna-sierra.org; historias de la ciencia; divulgamat2; pagina12.com; agnesscot.com; y en los muy buenos enlaces pbs.org. y la enciclopedia.com.
Para los franceses es, casi con toda seguridad, la mujer con mayor altura intelectual y científica de su historia, junto a Émilie du Châtelet. Se interesó no sólo por las Matemáticas y la Física; también por la Filosofía, la Química, la Geografía y la Historia. Incluso, hoy día, estudiosos de sus manuscritos apuntan a que en ellos hay bastante más de lo que parece; urge por tanto revisarlos. Fue honrada de distintas maneras –pero nunca como se merecía-: una calle en París, una escuela también en París y la casa donde murió fue convertida en monumento histórico, el Instituto de Francia concede anualmente el premio “ Le prix Sophie Germain” al investigador en Matemáticas más sobresaliente,entre otros.
Sin embargo la colección de “feos” a lo largo de su vida no paró ni después de su muerte: al construir la Torre Eiffel fueron incluidos los nombres de los setenta y dos sabios (ingenieros y cientificos) franceses más importantes (¡¡¡todos varones!!!!) no aparecía el nombre de Sophie Germain, que casualmente contribuyó a los avances de la ¡¡¡teoría de la elasticidad de los metales!!! Desde entonces hasta hoy la situación de la mujer en la ciencia ha cambiado mucho, muchísimo, pero todavía no al mismo nivel , según que países. Leemos por algún foro: “ es difícil ser mujer en el mundo de la ciencia”. Todavía deben seguir cambiando los modos y los modelos para que los desprecios por la capacidad intelectual femenina sea, sólo, un mal recuerdo del pasado. ¡Pero que muy pasado! AMJ
3 comentarios
sofia -
sofia -
anonimo -