El triángulo de Reuleaux y el arte.

(Casa Golferichs,1900. Barcelona)
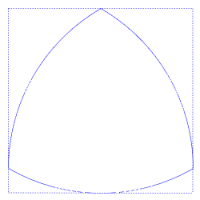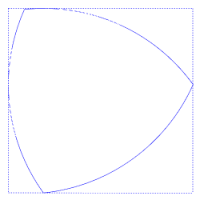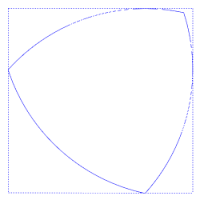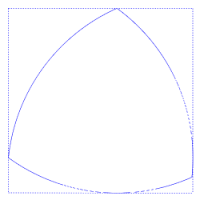
El triángulo de Reuleaux es el más sencillo de los polígonos de Reuleaux, que deben su nombre al científico Franz Reuleaux(1829, 1905), que fue quien los desarrolló. Es una curva de anchura constante –al igual que el resto de los polígonos- basada en un triángulo rectángulo. Se construye haciendo centro en uno de los vértices y radio “a” y trazando un arco de circunferencia que una los otros dos vértices del triángulo; y se repite con los otros dos vértices. Es el que tiene menor área que cualquier otra figura de anchura constante. Si “a” es la anchura constante, su área es 0,70477 a2 . Si “a” es el lado del triángulo equilátero que lo genera, su perímetro es Π·a.
 |
Pero no solo por su uso como una broca, al rodar fácilmente – aunque no se puede utilizar como rueda- es conocido este triángulo. En el arte se ha utilizado bastante. Veamos en las siguientes imágenes, y lugares donde se encuentra:
Iglesia de Notre Dame. Brujas(Bélgica) |
Catedral de Valencia. |
Catedral de Bilbao. |
Catedral de León. |
Iglesia de San Juan. Valencia | Iglesia Scots Union. Adelaida. |
Notre Dame. Luxemburgo. | Sagrada Familia. Barcelona. |
Hospitaalmuseum. Brujas(Bélgica). |
Gante. Bélgica. |
Catedral de San Salvador. Brujas. |
Iglesia Saint Didier. Avignon |

(Moreton Corbet, UK)

(Parroquia de Santa Cruz. Madrid)
Sin duda todo un hallazgo de estas figuras de anchura constante. AMJ












0 comentarios