Joseph Louis Lagrange, uno de los grandes.

Tres lugares orientan la vida de  Joseph Louis Lagrange: Turín –donde nació y vivió sus treinta primeros años de vida- , Berlín –donde vivió desde 1766 a 1787-  y París –donde vivió desde 1788 hasta su muerte en 1813-. Su nacionalidad fue puesta en entredicho durante bastante tiempo, pero durante la Revolución francesa adquirió la categoría de ciudadano francés, pues aunque nació en el Piamonte italiano, procedía de una familia parisina de alta posición social. A los 18 años era ya un matemático consumado y un año más tarde resolvió un problema que llevaba medio siglo sin resolver -el famoso problema isoperimétrico -, utilizando cálculo de variaciones. La comunicación con Euler de este trabajo supuso su encumbramiento entre los grandes matemáticos europeos, con solo 19 años. Su dedicación exclusiva e insistente en el campo de la matemática- de lo cual no tenía rival en Europa-, lo hizo un individuo enfermizo. De complexión débil, padeció problemas nerviosos el resto de su vida, acompañado de profundas depresiones. Su alejamiento de las disputas y controversias científicas hizo que otros se aprovecharan de sus avances y logros matemáticos.

 No quiso ir a Berlín mientras Euler estuviese por allí(¿quizás el desinterés que el alemán mostró por él?), pese a la insistencia de éste y de D’Alambert. Una vez que en 1766 Euler abandonó Berlín, el rey de Prusia Federico II el Grande quería tener a su lado “al más grande matemático europeo” y en los siguientes 20 años, Lagrange trabajó y produjo una serie impresionante de trabajos matemáticos y físicos. Además publicó su obra culmen: Mécanique Analytique.                 

La muerte de su esposa, al poco tiempo de casarse le afectó bastante a su producción científica y sobre todo tuvo que  adaptar su trabajo científico a su ritmo vital -el exceso de té y café para mantenerse despierto en su juventud le habían pasado factura "estomacal"-, ya que en exceso, le producía enfermedad –se cree que era lo que ahora se llama estrés-.

 Se instala más tarde en París- después de la muerte de Federico II- tras la llamada de Luis XVI pero le alarmó bastante los resultados de la Revolución Francesa –aunque siempre fue respetado por los revolucionarios, que le cubrieron de honores y distinciones-. Napoleón decía de él:"Lagrange es la pirámide de la ciencia matemática" además de nombrarlo Senador, Conde del Imperio y Oficial de la Legión de Honor. La muerte de Lavoisier en la guillotina le pñrodujo estupefacción y dijo de ella:"Bastará sólo un momento para que su cabeza caiga, y quizá sea necesario un centenar de años, para que se produzca otra igual" Cuando iba a marcharse le ofrecieron la presidencia de la Comisión de pesos y medidas. Fue nombrado profesor de la École polytecnique y más tarde una plaza honorífica en la École Normal.  Cuando estaba revisando su obra magna Mécanique analytique murió en 1813. Dos días antes de su muerte, sabiéndose bastante enfermo, les decía a sus amigos que le visitaron -Monge entre ellos-:"He obtenido alguna celebridad en Matemática. No he odiado a nadie. No he hecho ningún mal y es hora de terminar".

 Entre sus contribuciones está la Miscellanea Turinesa, una enciclopedia de cinco volúmenes de su época en Turín y contiene, mayormente, resultados aplicables a la Física (propagación del sonido, series recursivas, probabilidad, cálculo de variaciones, dinámica, cálculo integral, una solución del problema de Fermat y el Problema de los tres cuerpos).

  Ya en Berlín continuó con su Miscellanea e introdujo soluciones a problemas de Astronomía, fluidos y la integración de una serie infinita.

 Trabajó en el terreno del Álgebra –formas cuadrática eliminación de parámetros, resolución de ecuaciones algebraicas, ecuaciones binomiales y determinantes, entre otros apartados- y de la Teoría de Números – demostración del teorema de Wilson y otros de Fermat-.

En Física reformuló la mecánica de Newton para simplificar fórmulas y procedimientos y facilitar cálculos. Es la conocida como mecánica Lagrangeana -"el mejor ejemplo de hacer arte de la nada", o como dijo Hamilton "una especie de poema científico"-.

Escribió numerosos artículos sobre Geometría Analítica, Ecuaciones Diferenciales, la prueba del Teorema de Taylor, el uso de los infinitesimales en el Cálculo Diferencial, Aproximación de raíces por fracciones continuas, etc. A él se le deben los símbolos f’(x),f’’(x) ,... así como la palabra derivada.

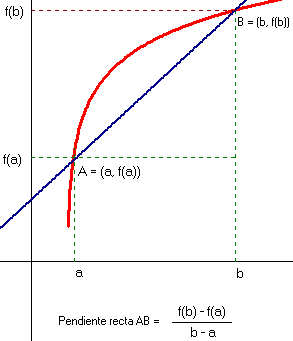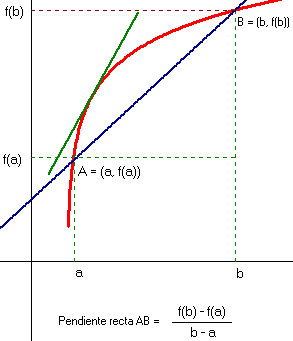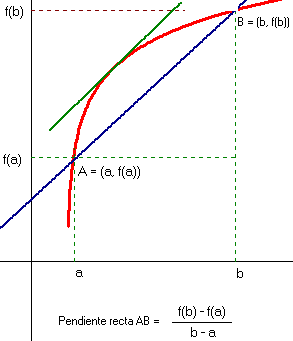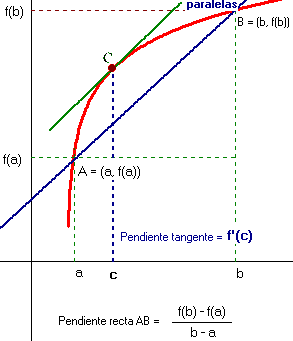
 Para un autor tan prolífico –tocó todas las ramas de las matemáticas y la física- que se dedicó fundamentalmente a la matemática pura lo que ha quedado de él es bastante poco( El Teorema de Lagrange, la Mecánica Lagrangeana, el Polinomio de Lagrange,…), incluso en el Bachillerato se estudia el Teorema de los incrementos infinitos de Lagrange y todo el mundo lo conoce como el teorema del valor medio. Muchos de los que le rodearon se aprovecharon de su dedicación a la matemática pura, y esos resultados fueron aprovechados por otros para aplicarlos a circunstancias menos abstractas. Esto no le importó a Joseph Louis, un genio en Teoría de Números, a la altura de Diofanto o Fermat.

Más sobre su biografía en Universidad de Granada, history.mcs, librosmaravillosos.com (muy completa), astromia.com o rauljara.com .

 Si repasamos todo lo que hizo, lo que avanzó la Ciencia con su contribución, creemos que su pertenencia a la época donde las Matemáticas en Francia gozaron de su mayor esplendor (Gaspar Monge, Adrien M. Legendre, Laplace, Bernouilli,  D’Alambert, Cauchy,…) ha hecho que su nombre haya quedado un poco apagado, pero debe ser considerado como uno de los grandes. Estos días se celebran exposiciones en París y otros lugares de Francia exposiciones con material de Lagrange,: cartas, comunicaciones entre investigadores, fotos, etc, que enlazamos en Images de Mathematiques. En nuestras clases lo recordamos, para que se tenga una visión  de la Historia de la Matemática lo menos sesgada posible y sobre todo, el dejar patente la cantidad y calidad de la "cosecha matemática" que produjo este insigne científico, casi prostrado en el "arcén de la matemática". AMJ