La banda de Möebius
Es una superficie un tanto "rara". Presenta unas propiedades llamaríamoslas extrañas como: tiene una sola cara, un solo borde, no es orientable. Si se corta a lo largo en la mitad del ancho de la cinta se obtiene una banda más larga pero con dos vueltas. Si a esta banda que hemos obtenido se la vuelve a cortar por la mitad obtenemos dos bandas entrelazadas. Geométricamente se pueden dar sus ecuaciones en paramétricas:
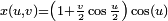
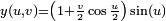
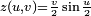
Como curiosidad apuntar que Johan Sebastian Bach compuso un canon cuya partitura, al ejecutarse, guarda semejanza con la forma de una Banda de Möbius.
En este enlace se puede profundizar un poco más:
http://es.wikipedia.org/wiki/Banda_de_M%C3%B6bius
En el video vemos cuatro experimentos con la banda de Möebius.
De Abc Maths Blog.
Comentarios » Ir a formulario
Autor: Quelo
