Lothar Collatz y su conjetura(¿conexión con el KGB?).

Un día como hoy, 26 de Septiembre, de 1990, murió, a los 80 años, en Varna (Bulgaria)(¡preciosa ciudad a orillas del Mar Negro!) este matemático alemán conocido por su famosa conjetura, llamada conjetura de Collatz( o también de Siracusa), enunciada en 1937 y que todavía no ha tenido solución(demostración en un sentido o en otro).
Algunos de los mejores matemáticos americanos pensaron que Collatz era un agente del KGB: su conjetura era, de hecho, el arma de una conspiración destinada a desacreditar la verdadera investigación matemática de EEUU(¡parece de libro de ciencia ficción!). La conjetura queda de la siguiente forma (tomada de la Wikipedia):
Sea la siguiente operación, aplicable a cualquier número entero positivo:
- Si el número es par, se divide entre 2.
- Si el número es impar, se multiplica por 3 y se suma 1.
Formalmente, esto equivale a una función 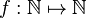 :
:
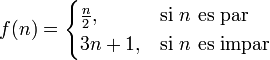
Dado un número cualquiera, podemos considerar su órbita es decir, las imágenes sucesivas al iterar la función. Por ejemplo, si n=13:
Si observamos este ejemplo, la órbita de 13 es periódica, es decir, se repite indefinidamente a partir de un momento dado):
13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,...
La conjetura dice que siempre alcanzaremos el 1 (y por tanto el ciclo 4, 2, 1) para cualquier número con el que comencemos. Ejemplos:
- Comenzando en n = 6, uno llega a la siguiente sucesión: 6, 3, 10, 5, 16, 8, 4, 2, 1.
- Empezando en n = 11, la sucesión tarda un poco más en alcanzar el 1: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
 Hay un proyecto para calcular el número más grande posible obtenido en una sucesión de Collatz( el proyecto es BOINC 3x+1@home). En Agosto se encontró el número 2.361.235.441.021.745.907.775.
Hay un proyecto para calcular el número más grande posible obtenido en una sucesión de Collatz( el proyecto es BOINC 3x+1@home). En Agosto se encontró el número 2.361.235.441.021.745.907.775.AMJ
1 comentario
dulcemar -