El problema del junquillo chino.
El Junquillo Chino
El siguiente problema fue hallado en el capítulo IX del libro chino: "Chu Chang Suan Shu" o "Arte Matemático en Nueve Secciones" .
Crece en medio de una laguna circular de 3m (300cm) de diámetro un junquillo que sobresale 30 cm del agua cuando se inclina hasta que lo cubre de agua alcanza justamente la orilla de la laguna, ¿qué profundidad tiene el agua?
Este antiguo libro chino data probablemente del siglo II a.C (Dinastía Han) y contiene 246 problemas divididos en 9 capítulos, el autor es desconocido , y contiene el resumen de todo el conocimiento matemático poseído en China hasta la primera mitad del siglo III d.C. algunos de estos problemas datan de la Dinastía Qin (221 - 220 a.C.) y fueron compilados por Zhang Cang (256? - 152 a.C.)
El libro tuvo numerosos comentaristas tales como el matemático chino Lui Hiu quien escribió en el año 263 a.C un comentario donde proveyó la justificación matemática para las reglas y soluciones de los problemas escritos allí, además de otros como Zu Kengzhi (siglo VI d.C.), de li Chunfeng (602-670) y de Yang Hui (1270).
Veamos la solución del problema propuesto: graficando las condiciones del problema antes de que el junquillo se inclinara:
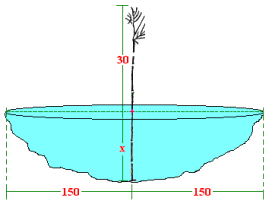
Como 300 cm es el diámetro de la laguna entonces la distancia del junquillo a la orilla es de 150 cm. Además que la profundidad del agua estará dado por x que es también la longitud de la parte sumergida del junquillo, téngase en cuenta que la longitud total del junquillo es x + 30.
Grafiquemos nuevamente ahora teniendo en cuenta la inclinación del junquillo precisamente cuando su extremo superior alcanza la orilla.
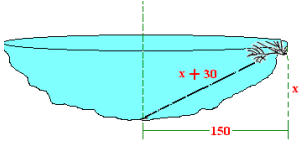
Por el teorema de Pitágoras:
luego x = 360 cm = 3,6 m
Este problema muy posiblemente haya pasado de La China a la India y en efecto es así pues Bhaskara II (llamado también Bhaskaracharya ) en su Lilavati expone este problema de manera ligeramente diferente por ejemplo en vez de considerar un junquillo como el protagonista del problema Bhaskara optó por elegir una planta familiar de su territorio como el loto, veamos:
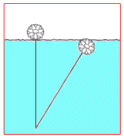En cierto lago, el repleto de gansos rosados y grullas, se podían ver, la parte superior de una flor de una planta de loto un palmo arriba de la superficie del agua. Forzado por el viento, avanzó gradualmente y fue sumergido por el agua a una distancia de 4 palmos. (ver figura)
Calcula, deprisa matemático ¡¡¡¡¡ la profundidad del agua.
El Lilavati (que significa "El Hermoso") es el manuscrito más conocido escrito por Bhaskara II en el año 1150 d.C a los 36 años de edad y contiene 278 versos sobre diversos aspectos de las matemáticas hindúes como por ejemplo: resolución de ecuaciones cuadráticas, progresiones, el teorema de Pitágoras, regla de tres, medición de volúmenes, etc.
Bhaskara II también escribió el Bijaganita (semilla que cuenta o extrae la raíz) en la que expone temas del álgebra; el Siddhantasiromani que está dividido en dos partes: la primera parte trata sobre astronomía matemática y la segunda sobre la esfera; el Vasanabhasya de Mitaksara que es un comentario propio del Siddhantasiromani; el Karanakutuhala (cálculo de maravillas astronómicas) o Brahmatulya que son una versión simplificada del Siddhantasiromani; y el Vivarana de el cual es un comentario en el Shishyadhividdhidatantra de Lalla.
2 comentarios
regwefg -
zxdx -